题目内容
4.已知Sn为数列{an}的前n项和,且满足an=2Sn-1+2(n≥2);数列{bn}满足b1+b2+b3+…+bn=n2+n.(1)数列{an}是等比数列吗?请说明理由;
(Ⅱ)若a1=b1,求数列{an•bn}的前n项和Tn.
分析 (1)an=2Sn-1+2(n≥2),利用递推关系可得:an+1=3an.n=2时,a2=2a1+2,只有当a1=2时,满足a2=3a1,即可判断出结论.
(II)利用递推关系、“错位相减法”即可得出.
解答 解:(1)∵an=2Sn-1+2(n≥2),an+1-an=(2Sn+2)-(2Sn-1+2)=2an,化为an+1=3an.
n=2时,a2=2a1+2,只有当a1=2时,a2=6=3a1,
此时数列{an}是等比数列,否则不是等比数列.
(II)∵数列{bn}满足b1+b2+b3+…+bn=n2+n,
∴n=1时,b1=2=a1,
n≥2时,bn=n2+n-[(n-1)2+(n-1)]=2n,n=1时也成立.
∴bn=2n.
此时数列{an}是等比数列,首项为2,公比为3.
∴an=2×3n-1.
∴anbn=4n×3n-1.
∴数列{an•bn}的前n项和Tn=4(1+2×3+3×32+…+n×3n-1),
3Tn=4(3+2×32+…+n×3n),
∴-2Tn=4(1+3+32+…+3n-1-n×3n)=4×$(\frac{{3}^{n}-1}{3-1}-n×{3}^{n})$,
∴Tn=(2n-1)×3n+1.
点评 本题考查了递推关系、“错位相减法”、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.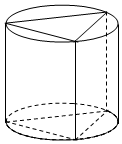 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )| A. | 6$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
13.若a,b,c,d均为正实数,且c是a和b的等差中项,d是a和b的等比中项,则有( )
| A. | ab>cd | B. | ab≥cd | C. | ab<cd | D. | ab≤cd |