题目内容
16．在△ABC中，根据下列条件，求三角形的面积S．（1）已知a=3cm，c=4cm，B=30°；
（2）已知A=75°，C=45°，b=4cm．
分析 （1）把已知数据代入三角形的面积公式计算可得；
（2）由题意可得B=60°，由正弦定理可得c，由和差角的三角函数公式可得sinA，代入三角形的面积公式计算可得．
解答 解：（1）∵在△ABC中a=3cm，c=4cm，B=30°，
∴三角形的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×3×4×$\frac{1}{2}$=3cm2；
（2）∵在△ABC中A=75°，C=45°，b=4cm，
∴B=180°-（75°+45°）=60°，
由正弦定理可得c=$\frac{bsinC}{sinB}$=$\frac{4×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{4\sqrt{6}}{3}$cm，
∴sinA=sin（B+C）=$\frac{\sqrt{2}}{2}×\frac{1}{2}$+$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$，
∴三角形的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×4×$\frac{4\sqrt{6}}{3}$×$\frac{\sqrt{2}+\sqrt{6}}{4}$=$\frac{12+4\sqrt{3}}{3}$cm2
点评 本题考查正弦定理解三角形，涉及三角形的面积公式及和差角的三角函数公式，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．设两条直线的方程分别为x+$\sqrt{3}$y+a=0，x+$\sqrt{3}$y+b=0，已知a，b是方程x2+2x+c=0的两个实根，且0≤c≤$\frac{1}{2}$，则这两条直线之间的距离的最大值和最小值的差为（ ）
| A． | $\frac{{2-\sqrt{2}}}{2}$ | B． | 1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{4-\sqrt{14}}}{4}$ |
11．
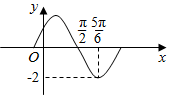函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则f（$\frac{19π}{6}$）的值为（ ）
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则f（$\frac{19π}{6}$）的值为（ ）| A． | 0 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | -$\sqrt{2}$ |