题目内容
19．若2${A}_{n}^{3}$=3${A}_{n+1}^{2}$-8${A}_{n}^{1}$，则n的值为3．分析 利用排列数公式可知n≥3，进而化简可知2n（n-1）（n-2）=3n（n+1）-8n，问题转化为解关于n的一元二次方程，进而计算可得结论．
解答 解：∵2${A}_{n}^{3}$=3${A}_{n+1}^{2}$-8${A}_{n}^{1}$，
∴n≥3，且2n（n-1）（n-2）=3n（n+1）-8n，
整理得：2n2-9n+9=0，
解得：n=3或n=$\frac{3}{2}$（舍），
故答案为：3．
点评 本题考查排列及排列数公式，考查运算求解能力，注意解题方法的积累，属于中档题．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
9．已知等差数列{an}满足an∈N*，且前10项和S10=280，则a9的最大值为（ ）
| A． | 29 | B． | 49 | C． | 50 | D． | 58 |
7．设两条直线的方程分别为x+$\sqrt{3}$y+a=0，x+$\sqrt{3}$y+b=0，已知a，b是方程x2+2x+c=0的两个实根，且0≤c≤$\frac{1}{2}$，则这两条直线之间的距离的最大值和最小值的差为（ ）
| A． | $\frac{{2-\sqrt{2}}}{2}$ | B． | 1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{4-\sqrt{14}}}{4}$ |
11．
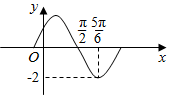函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则f（$\frac{19π}{6}$）的值为（ ）
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0）的部分图象如图所示，则f（$\frac{19π}{6}$）的值为（ ）| A． | 0 | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | -$\sqrt{2}$ |