题目内容
已知函数f(x)=x2+(a-1)x+a为偶函数.
(1)求a的值;
(2)设函数,g(x)=
,当x∈[1,+∞]时,不等式g(x)+f(m)+2m≥5恒成立,求m的取值范围.
(1)求a的值;
(2)设函数,g(x)=
| f(x) |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)利用偶函数的性质,f(-x)=f(x),可求得a的值;
(2)依题意,当x∈[1,+∞)时,不等式g(x)+f(m)+2m≥5恒成立?-m2-2m+4≤x+
恒成立,构造函数h(x)=x+
,利用双钩函数的单调性质可求得h(x)min,从而解不等式-m2-2m+4≤h(x)min,即可.
(2)依题意,当x∈[1,+∞)时,不等式g(x)+f(m)+2m≥5恒成立?-m2-2m+4≤x+
| 1 |
| x |
| 1 |
| x |
解答:
解:(1)∵f(x)=x2+(a-1)x+a为偶函数,
∴f(-x)=(-x)2+(a-1)•(-x)+a=x2-(a-1)x+a=x2+(a-1)x+a=f(x),
∴2(a-1)x=0恒成立,故a=1;
(2)由(1)知,a=1,f(x)=x2+1,
∴g(x)=
=x+
,
∵当x∈[1,+∞)时,不等式g(x)+f(m)+2m≥5恒成立?x∈[1,+∞)时,x+
+m2+1+2m≥5恒成立?x∈[1,+∞)时,-m2-2m+4≤x+
恒成立,
令h(x)=x+
,
则x∈[1,+∞)时,-m2-2m+4≤h(x)min,
∵双钩函数h(x)=x+
在区间[1,+∞)上单调递增,
∴h(x)min=h(1)=2,
∴-m2-2m+4≤2,即m2+2m-2≥0,
解得:m≥
-1或m≤-
-1.
∴m的取值范围是(-∞,-1-
]∪[
-1,+∞).
∴f(-x)=(-x)2+(a-1)•(-x)+a=x2-(a-1)x+a=x2+(a-1)x+a=f(x),
∴2(a-1)x=0恒成立,故a=1;
(2)由(1)知,a=1,f(x)=x2+1,
∴g(x)=
| f(x) |
| x |
| 1 |
| x |
∵当x∈[1,+∞)时,不等式g(x)+f(m)+2m≥5恒成立?x∈[1,+∞)时,x+
| 1 |
| x |
| 1 |
| x |
令h(x)=x+
| 1 |
| x |
则x∈[1,+∞)时,-m2-2m+4≤h(x)min,
∵双钩函数h(x)=x+
| 1 |
| x |
∴h(x)min=h(1)=2,
∴-m2-2m+4≤2,即m2+2m-2≥0,
解得:m≥
| 3 |
| 3 |
∴m的取值范围是(-∞,-1-
| 3 |
| 3 |
点评:本题考查函数恒成立问题,考查函数的奇偶性单调性与最值,考查构造函数思想与等价转化思想的综合运用,属于难题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
复数=z=i3(1+i)(i为虚数单位)在复平面上对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
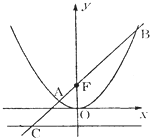 如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )
如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )| A、x2=4y |
| B、x2=8 y |
| C、x2=2y |
| D、x2=16y |