题目内容
5.下列函数中,在区间(0,+∞)上是增函数的是( )| A. | y=-4x+5 | B. | y=9-x2 | C. | y=($\frac{1}{2}$)x | D. | y=|x| |
分析 根据一次函数、二次函数、指数函数的单调性便可判断每个选项函数在(0,+∞)上的单调性,从而找出正确选项.
解答 解:A.y=-4x+5在(0,+∞)上为减函数,∴该选项错误;
B.由y=9-x2的图象知,该函数在(0,+∞)上为减函数,∴该选项错误;
C.指数函数$y=(\frac{1}{2})^{x}$在(0,+∞)上为减函数,∴该选项错误;
D.x>0时,y=|x|=x为增函数,∴该选项正确.
故选:D.
点评 考查一次函数,二次函数,及指数函数的单调性,要熟悉每个选项函数的图象,根据函数图象判断函数单调性的方法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13.过点$P(-\sqrt{3},-1)$的直线l与圆x2+y2=1有公共点,则直线l的斜率的取值范围是( )
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\sqrt{3}]$ | C. | $[0,\frac{{\sqrt{3}}}{3}]$ | D. | $[0,\sqrt{3}]$ |
20.已知函数f(x)=x3-3x2+1,g(x)=$\left\{\begin{array}{l}{x+\frac{1}{4x},x>0}\\{-x^2-6x-8,x≤0}\end{array}\right.$,则方程g[f(x)]-1=0的根的个数为( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
15.在甲、乙两个盒子中分别装有标号为1,2,3,4,5的五个球,现从甲乙两个盒子中各取出1个球,球的标号分别记做a,b,每个球被取出的可能性相等,则|a-b|≤1的概率为( )
| A. | $\frac{12}{25}$ | B. | $\frac{13}{25}$ | C. | $\frac{14}{25}$ | D. | $\frac{3}{5}$ |
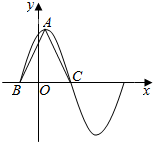 函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.