题目内容
16.已知直线l:kx-y+1=0(k∈R).若存在实数k,使直线l与曲线C交于A,B两点,且|AB|=|k|,则称曲线C具有性质P.给定下列三条曲线方程:①y=-|x|;
②x2+y2-2y=0;
③y=(x+1)2.
其中,具有性质P的曲线的序号是②③.
分析 确定直线l:kx-y+1=0(k∈R)过定点(0,1),曲线过定点(0,1),即可得出结论.
解答 解:①y=-|x|与直线l:kx-y+1=0(k∈R)至多一个交点,不具有性质P;
②x2+y2-2y=0圆心为(0,1),直线l:kx-y+1=0(k∈R)过定点(0,1),故存在k=±2,使直线l与曲线C交于A,B两点,且|AB|=|k|,具有性质P;
③y=(x+1)2,过点(0,1),直线l:kx-y+1=0(k∈R)过定点(0,1),故存在k,使直线l与曲线C交于A,B两点,且|AB|=|k|,具有性质P.
故答案为:②③.
点评 本题考查曲线与方程,考查新定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
1.给定函数①y=x${\;}^{\frac{1}{2}}$②y=log${\;}_{\frac{1}{2}}$(x+1)③y=|x2-2x|④y=($\frac{5}{6}$)x,其中在区间(0,1)上单调递减的函数序号是( )
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ①③ |
5.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-4x+5 | B. | y=9-x2 | C. | y=($\frac{1}{2}$)x | D. | y=|x| |
6.已知实数a,b,则“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.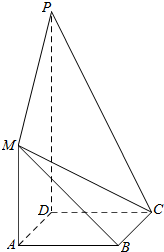 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.