题目内容
15.在甲、乙两个盒子中分别装有标号为1,2,3,4,5的五个球,现从甲乙两个盒子中各取出1个球,球的标号分别记做a,b,每个球被取出的可能性相等,则|a-b|≤1的概率为( )| A. | $\frac{12}{25}$ | B. | $\frac{13}{25}$ | C. | $\frac{14}{25}$ | D. | $\frac{3}{5}$ |
分析 所有的数对(a,b)共有5×5=25个,而满足|a-b|≤1的数对用列举法求得有13个,由此求得所求事件的概率.
解答 解:所有的数对(a,b)共有5×5=25个,而满足|a-b|≤1的数对(a,b)有(1,1),(1,2),(2,1)、(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),(4,5),(5,4),(5,5)共计13个,
故|a-b|≤1的概率为$\frac{13}{25}$
故选:B.
点评 本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-4x+5 | B. | y=9-x2 | C. | y=($\frac{1}{2}$)x | D. | y=|x| |
6.已知实数a,b,则“$\frac{1}{a}$>$\frac{1}{b}$”是“a<b”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
10.已知函数y=f(x)的图象是由函数$y=sin({2x+\frac{π}{6}})$的图象向左平移$\frac{π}{6}$个单位得到的,则$f({\frac{π}{3}})$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
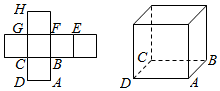 一个正方体的平面展开图及正方体的直观图的示意图如图所示:
一个正方体的平面展开图及正方体的直观图的示意图如图所示: