题目内容
1.已知函数f(x)=ex-1-$\frac{ax}{x-1}$,a∈R.(1)若函数g(x)=(x-1)f(x)在(0,1)上有且只有一个极值点,求a的范围;
(2)当a≤-1时,证明:f(x)<0对任意x∈(0,1)成立.
分析 (1)求出导函数,由题意可知f(x)在(0,1)上有且只有一个极值点,相当于导函数有一个零点;
(2)问题可转换为(x-1)(ex-1)-ax>0恒成立,构造函数G(x)=(x-1)(ex-1)-ax,通过二次求导,得出结论.
解答 解:(1)g(x)=(x-1)(ex-1)-ax,
g'(x)=xex-a-1,g''(x)=ex(x+1)>0,
∵f(x)在(0,1)上有且只有一个极值点,
∴g'(0)=-a-1<0,g'(1)=e-a-1>0,
∴-a<a<e-1;
(2)当a≤-1时,f(x)<0,
∴(x-1)(ex-1)-ax>0恒成立,
令G(x)=(x-1)(ex-1)-ax,
G'(x)=xex-a-1,G''(x)=ex(x+1)>0,
∴G'(x)在(0,1)单调递增,
∴G'(x)≥G'(0)=-a-1≥0,
∴G(x)在(0,1)单调递增,
∴G(x)≥G(0)=0,
∴(x-1)(ex-1)-ax≥0,
∴当a≤-1时,f(x)<0对任意x∈(0,1)成立.
点评 本题考查了极值点的概念和导函数的应用,难点是对导函数的二次求导.

练习册系列答案
相关题目
6.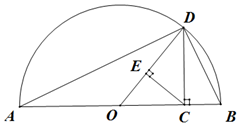 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )| A. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | B. | $CD,DE,\frac{2ab}{a+b}≤\sqrt{ab}$ | C. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | D. | $CD,CE,\frac{2ab}{a+b}≤\sqrt{ab}$ |
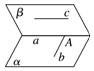 如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.
如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.