题目内容
12．
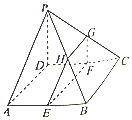如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD为菱形，．点分E，F，G，H别是棱AB，CD，PC，PB上共面的四点，且BC∥EF． 证明：GH∥EF．
分析 推导出BC∥平面EFGH，从而GH∥BC，由此能证明GH∥EF．
解答 （12分）
证明：∵BC∥EF，BC?平面EFGH，EF?平面EFGH，
∴BC∥平面EFGH，
∵BC?平面PBC，平面PBC∩平面EFGH=GH，
∴GH∥BC，
∵BC∥EF，∴GH∥EF．
点评 本题考查线线平行的证明，是基础题，解题时要认真审题，注意平行公理的合理运用．
练习册系列答案
相关题目
11．
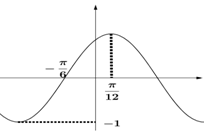已知f（x）=Asin（ωx+φ）（A＞0ω＞0，$|φ|＜\frac{π}{2}$，x∈R）在一个周期的图象如图所示，当$f（x）=\frac{1}{2}$时，$cos（2x-\frac{π}{6}）$=（ ）
已知f（x）=Asin（ωx+φ）（A＞0ω＞0，$|φ|＜\frac{π}{2}$，x∈R）在一个周期的图象如图所示，当$f（x）=\frac{1}{2}$时，$cos（2x-\frac{π}{6}）$=（ ）| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
20．等腰直角三角形AOB内接于抛物线y2=2px（p＞0），O为抛物线的顶点，OA⊥OB，△AOB的面积是16，抛物线的焦点为F，若M是抛物线上的动点，则$\frac{|OM|}{|MF|}$的最大值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{6}}{3}$ |
7．已知集合A={x|x2-2x＞0}，集合B={x|y=lg（x-1）}，则A∩B=（ ）
| A． | （1，+∞） | B． | （2，+∞） | C． | （-∞，0）∪（2，+∞） | D． | （-∞，0）∪（1，+∞） |
17．执行如图所示的程序框图后，输出s的值为（ ）
| A． | 8 | B． | 9 | C． | 30 | D． | 36 |
2．一元二次方程x2=4x的根是（ ）
| A． | 4 | B． | ±2 | C． | 0或2 | D． | 0或4 |