题目内容
17.执行如图所示的程序框图后,输出s的值为( )
| A. | 8 | B. | 9 | C. | 30 | D. | 36 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可得该程序的作用是利用循环计算并输出S值.模拟程序的运行过程,对程序运行过程中各变量的值进行分析,即可得到最终的输出结果.
解答 解:第一次循环,k=0≤3,S=0+0=0,k=1,
第二次循环,k=1≤3,S=0+1=1,k=2,
第三次循环,k=2≤3,S=1+8=9,k=3,
第四次循环,k=3≤3,S=9+27=36,k=4
不符合判断条件,输出S=36.
故选D.
点评 据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理);②建立数学模型,根据第一步分析的结果,选择恰当的数学模型;③解模型.属于基础题.

练习册系列答案
相关题目
16.某船在A处向正东方向航行xkm后到达B处,然后沿南偏西60°方向航行3km到达C处.若A与C相距$\sqrt{3}$km,则x的值是( )
| A. | 3 | B. | $\sqrt{3}$或2$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
8.已知函数f(x)=$\frac{1}{2}$x2-alnx(a>0)
(1)若f(x)在x=2处的切线与直线 3x-2y+1=0平行,求f(x)的单调区间
(2)求f(x)在区间[1,2]上的最小值.
(1)若f(x)在x=2处的切线与直线 3x-2y+1=0平行,求f(x)的单调区间
(2)求f(x)在区间[1,2]上的最小值.
2.若定义在R上的函数f(x)当且仅当存在有限个非零自变量x,使得f(-x)=f(x),则称f(x)为类偶函数.那么下列函数中,为类偶函数的是( )
| A. | f(x)=4cosx | B. | f(x)=x2-2x+3 | C. | f(x)=2x+1 | D. | f(x)=x3-3x |
9.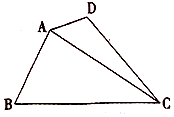 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
 如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )
如图,四边形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,则线段AC长度的取值范围是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |
6.定义两种运算:a⊕b=$\sqrt{{a}^{2}-{b}^{2}}$,a?b=$\sqrt{(a-b)^{2}}$,则f(x)=$\frac{2⊕x}{2-(x?2)}$是( )
| A. | 奇函数 | B. | 偶函数 | C. | 既奇又偶函数 | D. | 非奇非偶函数 |
7.下列程序语句不正确的是( )
| A. | INPUT“MATH=”;a | B. | PRINT“MATH=”;a+b+c | ||
| C. | y=b-c | D. | a+b=c |
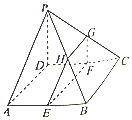 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.