题目内容
设实数x,y满足约束条件
,则u=
的取值范围是( )
|
| 2x+y |
| x+2y |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:简单线性规划的应用
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用数形结合将目标函数进行转化,利用直线的斜率结合分式函数的单调性即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
则对应的x>0,y>0,
则u=
=
,
设k=
,则u=
=
=
+
,
由图象可知当直线y=kx,经过点A(1,2)时,斜率k最大为k=2,
经过点B(3,1)时,斜率k最小为k=
,
即
≤k≤2.
∴
≤1+2k≤5,
≤
≤
,
∴
≤
≤
,
即
≤
+
≤
,
即
≤z≤
,
故选:C
则对应的x>0,y>0,
则u=
| 2x+y |
| x+2y |
2+
| ||
1+2•
|

设k=
| y |
| x |
| 2+k |
| 1+2k |
k+
| ||||
| 1+2k |
| 1 |
| 2 |
| ||
| 1+2k |
由图象可知当直线y=kx,经过点A(1,2)时,斜率k最大为k=2,
经过点B(3,1)时,斜率k最小为k=
| 1 |
| 3 |
即
| 1 |
| 3 |
∴
| 5 |
| 3 |
| 1 |
| 5 |
| 1 |
| 1+2k |
| 3 |
| 5 |
∴
| 3 |
| 10 |
| ||
| 1+2k |
| 9 |
| 10 |
即
| 4 |
| 5 |
| 1 |
| 2 |
| ||
| 1+2k |
| 7 |
| 5 |
即
| 4 |
| 5 |
| 7 |
| 5 |
故选:C
点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合是解决本题的关键,综合性较强,运算量较大.

练习册系列答案
相关题目
在等差数列{an}中,2a4+a7=2,则数列{an}的前9项和等于( )
| A、3 | B、9 | C、6 | D、12 |
设函数f(x)在R上存在导数f′(x),对任意的x∈R,有f(-x)+f(x)=x2,且x∈(0,+∞)时,f′(x)>x.若f(2-a)-f(a)≥2-2a,则实数a的取值范围为( )
| A、[1,+∞) |
| B、(-∞,1] |
| C、(-∞,2] |
| D、[2,+∞) |
若角α的终边与单位圆交于第三象限的一点P,其横坐标为-
,则tanα=( )
| ||
| 10 |
A、-
| ||
B、
| ||
| C、-3 | ||
| D、3 |
甲、乙两个工人每人加工一个零件,加工为一等品的概率分别为
和
,两个零件是否被加工为一等品互相独立,则这两个工人加工的两个零件中至少有一个一等品的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数y=f(x)(x∈R)的图象如图所示,则xf′(x)<0的解集为( )
已知函数y=f(x)(x∈R)的图象如图所示,则xf′(x)<0的解集为( )A、(-∞,
| ||||
B、(-∞,0)∪(
| ||||
C、(-∞,
| ||||
D、(-∞,
|
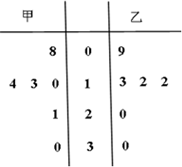 在如图所示的茎叶图中,甲、乙两组数据的平均数分别为
在如图所示的茎叶图中,甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
. |
| S甲 |
. |
| S乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
