题目内容
在等差数列{an}中,2a4+a7=2,则数列{an}的前9项和等于( )
| A、3 | B、9 | C、6 | D、12 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:根据等差数列的前n项和公式,即可得到结论.
解答:
解:在等差数列{an}中,2a4+a7=2,
则2(a1+3d)+a1+6d=2,
即3a1+12d=2,
∴a1+4d=
,
即a5=
,
∴S9=
=
=9×a5=9×
=6,
故选:C.
则2(a1+3d)+a1+6d=2,
即3a1+12d=2,
∴a1+4d=
| 2 |
| 3 |
即a5=
| 2 |
| 3 |
∴S9=
| 9(a1+a9) |
| 2 |
| 9×2a5 |
| 2 |
| 2 |
| 3 |
故选:C.
点评:本题主要考查等差数列的前n项的和的计算,根据条件求出a5=
是解决本题的关键.
| 2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
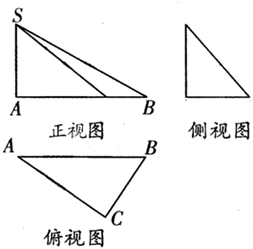 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
设全集为R,集合M={x∈R|f(x)≠0},N={x∈R|g(x)≠0},则集合{x∈R|f(x)•g(x)=0}等于( )
| A、(∁RM)∩(∁RN) |
| B、(∁RM)∪(∁RN) |
| C、M∪(∁RN) |
| D、(∁RM)∪N |
设实数x,y满足约束条件
,则u=
的取值范围是( )
|
| 2x+y |
| x+2y |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
命题:“?x∈R,2sinx≥1”的否定是( )
| A、?x∈R,2sinx<1 |
| B、?x∈R,2sinx≥1 |
| C、?x∈R,2sinx≤1 |
| D、?x∈R,2sinx<1 |
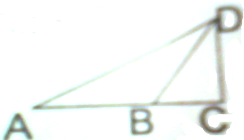 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100