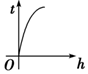题目内容
11.已知平面内动点C到点F(1,0)的距离比到直线$x=-\frac{1}{2}$的距离长$\frac{1}{2}$.(1)求动点C的轨迹方程E;
(2)已知点A(4,0),过点A的直线l与曲线E交于不同的两点P,Q,证明:以PQ为直径的圆过原点.
分析 (1)把直线x=-$\frac{1}{2}$向右平移$\frac{1}{2}$个单位变为x=-1,此时点P到直线x=-1的距离等于它到点(1,0)的距离,即可得到点P的轨迹方程.
(2)设出直线方程,联立直线与抛物线方程,利用韦达定理求解x1x2+y1y2=0,然后推出结论.
解答 解:(1)因为动点P到点(1,0)的距离比到直线$x=-\frac{1}{2}$的距离长$\frac{1}{2}$,
所以点P到直线x=-1的距离等于它到点(1,0)的距离,
因此点P的轨迹为抛物线,方程为y2=4x.
(2)证明:设过点A的直线l的斜率为:k,
直线PQ的方程为:y=k(x-4),设M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}{y=k(x-4)}\\{{y}^{2}=4x}\end{array}\right.$,消去y可得k2x2-8k2x-4x+16k2=0…①,
则x1x2=16,消去x可得:y2-$\frac{4}{k}$y-16=0,
y1y2=-16,
可得x1x2+y1y2=0,
即OM⊥ON,
所以,以PQ为直径的圆过原点.
点评 本题考查点P的轨迹方程,考查抛物线的定义,直线与抛物线的位置关系的综合应用,正确运用抛物线的定义是关键.

练习册系列答案
相关题目
1.命题甲:对任意x∈(a,b),有f′(x)>0;命题乙:f(x)在(a,b)内是单调递增的,则甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知a=0.30.3,b=1.20.3,c=log1.20.3,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
6.已知直线l的方向向量为$\vec s=(1,2,x)$,平面α的法向量$\vec n=(-2,y,2)$,若l?α,则xy的最大值为( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
20.等比数列{an}的前n项和为Sn,若a2+S3=0,则公比q=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
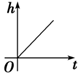
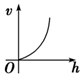
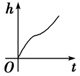
 如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )
如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )