��Ŀ����
1��������Ĭд���Ǻ��������ҹ�ʽ��C����+������C����-�����������ù�ʽC����-����֤����ʽC����+����C����+������cos����+�£�=cos��cos��-sin��sin�£�C����-������cos����-�£�=cos��cos��+sin��sin�£�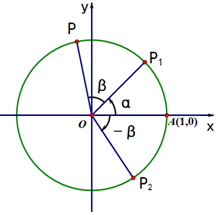
������ƽ��ֱ������ϵ�У�����A��x1��y1����B��x2��y2����ľ��빫ʽ�ǣ�$|{AB}|=\sqrt{{{��{{x_2}-{x_1}}��}^2}+{{��{{y_2}-{y_1}}��}^2}}$����ͼ����A��1��0����P1��cos����sin������P2��cos��-�£���sin��-�£�����P��cos����+�£���sin����+�£�����������ͼ�������Ƶ������Ǻ͵����ҹ�ʽ��C����+��������ע��������������������
���� �����ɦ�+��=��-��-�£��������յ���ʽ����֤����
������AP=P1P2�������ľ��빫ʽ���ɵý⣮
��� ����������Ϊ12�֣� �⣺�������Ǻ͵����ҹ�ʽC��+��Ϊ��cos����+�£�=cos��cos��-sin��sin�£����Dz�����ҹ�ʽC��-��Ϊ��cos����-�£�=cos��cos��+sin��sin�£�
�⣺�������Ǻ͵����ҹ�ʽC��+��Ϊ��cos����+�£�=cos��cos��-sin��sin�£����Dz�����ҹ�ʽC��-��Ϊ��cos����-�£�=cos��cos��+sin��sin�£�
֤������cos����-�£�=cos��cos��+sin��sin�£�
��cos����+�£�=cos[��-��-�£�]=cos��cos��-�£�+sin��sin��-�£�=cos��cos��-sin��sin�£���֤��
�ʴ�Ϊ��cos��cos��-sin��sin�£�cos��cos��+sin��sin�£�����6�֣�
������AP=P1P2�������ľ��빫ʽ���ã�[cos����+�£�-1]2+sin2����+�£�=[cos��-�£�-cos��]2+[sin��-�£�-sin��]2����6�֣�
չ���������ã�2-2cos����+�£�=2-2��cos��cos��-sin��sin�£�
��cos����+�£�=cos��cos��-sin��sin�£�����12�֣�
���� ���⿼�����Ǻ��������ҹ�ʽ�����������ľ��빫ʽ����������ǵ����Ǻ����Ķ���֤�����Ǻ͵����ҹ�ʽC��+�����ѵ㣬�����е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
12����֪����M={x|-3��x��1}��N={-3��-2��-1��0��1}����M��N���ڣ�������
| A�� | {-2��-1��0��1} | B�� | {-3��-2��-1��0} | C�� | {-2��-1��0} | D�� | {-3��-2��-1} |
6����a��[0��5]����x2+2ax+3a-2=0�����������ĸ���Ϊ��������
| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{3}{5}$ |