题目内容
已知数列{an}是等差数列，若a9+a12＞0，a10•a11＜0，且数列{an}的前n项和Sn有最大值，那么当Sn取得最小正值时，n等于（ ）
| A、17 | B、19 | C、20 | D、21 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由等差数列的性质和求和公式可得a10＞0，a11＜0，又可得S19=19a10＞0，而S20=10（a10+a11）＜0，进而可得Sn取得最小正值时n等于19．
解答：
解：∵a9+3a11＜0，∴由等差数列的性质可得
a9+3a11=a9+a11+2a11=a9+a11+a10+a12=2（a11+a10）＜0，
又a10•a11＜0，∴a10和a11异号，
又∵数列{an}的前n项和Sn有最大值，
∴数列{an}是递减的等差数列，
∴a10＞0，a11＜0，
∴S19=19a10＞0
∴S20=10（a1+a20）=10（a9+a12）＞0
∴Sn取得最小正值时n等于20
故选：C
a9+3a11=a9+a11+2a11=a9+a11+a10+a12=2（a11+a10）＜0，
又a10•a11＜0，∴a10和a11异号，
又∵数列{an}的前n项和Sn有最大值，
∴数列{an}是递减的等差数列，
∴a10＞0，a11＜0，
∴S19=19a10＞0
∴S20=10（a1+a20）=10（a9+a12）＞0
∴Sn取得最小正值时n等于20
故选：C
点评：本题考查等差数列的性质和求和公式，属基础题．
练习册系列答案
相关题目
若α∈（0，2π），且sinα+cosα=-
，则tanα=（ ）
| 7 |
| 5 |
A、±
| ||||
B、
| ||||
C、
| ||||
D、±
|
已知命题：?x＜0，0＜2x＜1，则￢p为（ ）
| A、?x＜0，2x≤0或2x≥1 |
| B、?x≥0，2x≤0或2x≥1 |
| C、?x≥0，0＜2x＜1 |
| D、?x＜0，2x≤0或2x≥1 |
已知椭圆
+
=1与双曲线
-
=1有相同的焦点，则动点P（n，m）的轨迹（ ）
| x2 |
| 9 |
| y2 |
| n |
| x2 |
| 4 |
| y2 |
| m |
| A、椭圆的一部分 |
| B、双曲线的一部分 |
| C、抛物线的一部分 |
| D、直线的一部分 |
下图是对数函数y=logax的图象，已知a的值取
、
、2、5，则相应于C1、C2、C3、C4的a的值依次是（ ）
| 1 |
| 3 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、5、2、
| ||||
D、5、2、
|
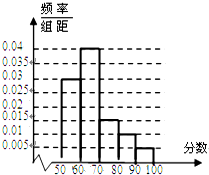在某中学举行的环保知识竞赛中，将三个年级参赛的学生的成绩进行整理后分为5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组，已知第二小组的频数是40，则成绩在80～100分的学生人数是（ ）