题目内容
若y=f(x)的定义域是[0,2],则函数f(x+1)的定义域是( )
| A、[-1,1] | ||||
B、[
| ||||
C、[
| ||||
D、[0,
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据题意可知0≤x+1≤2,求出x的范围并用区间表示,即可所求函数的定义域.
解答:
解:∵函数f(x)的定义域为[0,2],
∴0≤x+1≤2,解得-1≤x≤1,
∴所求函数y=f(x+1)的定义域是[-1,1],
故选:A.
∴0≤x+1≤2,解得-1≤x≤1,
∴所求函数y=f(x+1)的定义域是[-1,1],
故选:A.
点评:本题考查函数的定义域及其求法,属基础题,函数定义域为自变量x的范围,y=f(x)与y=f(t)的定义域相同.

练习册系列答案
相关题目
下列函数中,与函数y=x相同的函数是( )
| A、y=|x| | ||
B、y=
| ||
C、y=(
| ||
| D、y=logaax(a>0,且a≠1) |
已知向量
=(2k-3,-6),
=(2,1)且
∥
则实数k=( )
| a |
| c |
| a |
| c |
A、-
| ||
B、
| ||
| C、15 |
函数y=ln(x-2)的定义域是( )
| A、(-∞,+∞) |
| B、(-∞,2) |
| C、(0,2) |
| D、(2,+∞) |
把十进制数15化为二进制数为( )
| A、1 011(2) |
| B、1 001(2) |
| C、1 111(2) |
| D、1 101(2) |
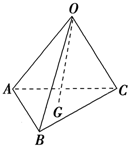 如图,在三棱锥O-ABC中,G是△ABC的重心,若
如图,在三棱锥O-ABC中,G是△ABC的重心,若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |
若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
,则直线l的斜率的取值范围是( )
| 2 |
A、[2-
| ||||||
B、[2-
| ||||||
C、[
| ||||||
| D、[0,+∞) |