题目内容
已知函数f(x)=
,记f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,则f2014(10)=( )
|
| A、10 | B、lg110 | C、0 | D、1 |
考点:函数的值
专题:函数的性质及应用
分析:由已知得f3n+m(10)=fm(10),m,n∈N*,由此推导出f2014(10)=f1(10)=f(10)=lg10=1.
解答:
解:∵函数f(x)=
,
∴f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,
∴f1(10)=f(10)=lg10=1,
f2(10)=f(f1(10))=f(1)=lg1=0,
f3(10)=f(f2(10))=f(0)=10,
f4(10)=f(f3(10))=f(10)=lg10=1,
∴f3n+m(10)=fm(10),m,n∈N*,
∵2014=671×3+1,
∴f2014(10)=f1(10)=f(10)=lg10=1.
故答案:D.
|
∴f1(x)=f(x),f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,
∴f1(10)=f(10)=lg10=1,
f2(10)=f(f1(10))=f(1)=lg1=0,
f3(10)=f(f2(10))=f(0)=10,
f4(10)=f(f3(10))=f(10)=lg10=1,
∴f3n+m(10)=fm(10),m,n∈N*,
∵2014=671×3+1,
∴f2014(10)=f1(10)=f(10)=lg10=1.
故答案:D.
点评:本题考查函数值的求法,是基础题,解题时要注意函数的周期性的合理运用.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
把十进制数15化为二进制数为( )
| A、1 011(2) |
| B、1 001(2) |
| C、1 111(2) |
| D、1 101(2) |
已知函数y=2x,g(x)=f(x-2)-1,若g(a)<1<f(a),则实数a的取值范围为( )
| A、(-∞,0)∪(3,+∞) |
| B、(-∞,0) |
| C、(0,3) |
| D、(0,+∞) |
若圆x2+y2-4x-4y-10=0上至少有三个不同点到直线l:ax+by=0的距离为2
,则直线l的斜率的取值范围是( )
| 2 |
A、[2-
| ||||||
B、[2-
| ||||||
C、[
| ||||||
| D、[0,+∞) |
若 a>b,则下列不等式正确的是( )
| A、a2>b2 |
| B、ab>ac |
| C、a-c>b-c |
| D、ac2>bc2 |
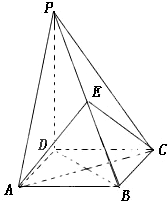 如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=
如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=