题目内容
3.在如图1所示的平面图形中,△ADE是等腰三角形且AE=DE=$\sqrt{5}$,四边形ABCD为矩形,AD=2,CD=$\sqrt{2}$,△BCF为直角三角形.把△ADE与△BCF分别沿AD、BC折成如图2所示的几何体,且平面ADE⊥平面ABCD,CF⊥平面ABCD,
(1)求证:BD⊥EF;
(2)若CF=1,试求EF与面BDE所成角的正弦值.
分析 (1)取AD中点H,连接EH、CH,说明AD⊥EH,证明EH⊥平面ABCD,说明E,H,C,F四点共面.证明DCH=∠CBD,推出BD⊥CH;证明BD⊥面EHCF,推出BD⊥EF.
(2)以C为原点,CD为x轴,CB为y轴,CF为z轴建立空间直角坐标系.求出平面BDE的法向量,然后利用空间向量的数量积求解EF与面BDE所成角的正弦值.
解答 (本小题满分12分)
证明:(1)取AD中点H,连接EH、CH,
由△ADE是等边三角形知:AD⊥EH,…(1分)
∵平面ADE⊥平面ABCD,AD为面ADE与面ABCD的交线,
∴EH⊥平面ABCD,…(2分)
而CF⊥平面ABCD,故EH∥CF,从而E,H,C,F四点共面. …(3分)
在Rt△DCH中,$tan∠DCH=\frac{DH}{DC}=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$;
在Rt△DCB中,$tan∠CBD=\frac{CD}{BC}=\frac{{\sqrt{2}}}{2}$,
∴∠DCH=∠CBD,…(4分)
∴∠DCH+∠BDC=∠CBD+∠BDC=90°,则BD⊥CH;…(5分)
∴BD⊥面EHCF,
∴BD⊥EF.…(6分)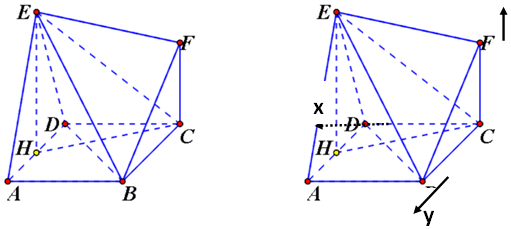
解:(2)以C为原点,CD为x轴,CB为y轴,CF为z轴建立空间直角坐标系.
在Rt△EDH中,$EH=\sqrt{E{D^2}-D{H^2}}=\sqrt{{{(\sqrt{5})}^2}-{1^2}}=2$,…(7分)
则:B(0,2,0),$D({\sqrt{2}_{\;}},{0_{\;}},0)$,$E(\sqrt{2},1,2)$,F(0,0,1),
则:$\overrightarrow{BD}=(\sqrt{2},-2,0)$,$\overrightarrow{BE}=(\sqrt{2},-1,2)$,$\overrightarrow{EF}=(-\sqrt{2},-1,-1)$,…(8分)
设平面BDE的法向量为$\overrightarrow n=(x,y,z)$,由$\overrightarrow n⊥{\overrightarrow{BD}_{\;}},\overrightarrow n⊥\overrightarrow{BE}$得:$\left\{{\begin{array}{l}{\sqrt{2}x-2y=0}\\{\sqrt{2}x-y+2z=0}\end{array}}\right.$,
解得:$\left\{{\begin{array}{l}{x=\sqrt{2}y}\\{z=-\frac{1}{2}y}\end{array}}\right.$,令y=2,则:$\overrightarrow n=(2\sqrt{2},2,-1)$,…(10分)
则$cos<\overrightarrow{EF},\overrightarrow n>=\frac{-4-2+1}{{2×\sqrt{13}}}=-\frac{{5\sqrt{13}}}{26}$,
∴EF与面BDE所成角的正弦值为$\frac{{5\sqrt{13}}}{26}$. …(12分)
点评 本题考查直线与平面所成角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
| A. | k≥8 | B. | k>8 | C. | k≥7 | D. | k>9 |
| A. | -e | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | e |
 如图,在四棱柱ABCD-A1B1C1D1中,已知AB=1,AA1=2,S是A1C1的中点
如图,在四棱柱ABCD-A1B1C1D1中,已知AB=1,AA1=2,S是A1C1的中点