题目内容
15.已知tanα=2,求$\frac{1}{1+sinα}$+$\frac{1}{1-sinα}$的值.分析 $\frac{1}{1+sinα}$+$\frac{1}{1-sinα}$=$\frac{2}{co{s}^{2}α}$=2(tan2α+1),代入计算,即可得出结论.
解答 解:∵tanα=2,
∴$\frac{1}{1+sinα}$+$\frac{1}{1-sinα}$=$\frac{2}{co{s}^{2}α}$=2(tan2α+1)=10.
点评 本题考查同角三角函数关系,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
4.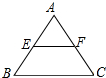 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.已知平面α截一球面得圆M,过圆心M且与α成30°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )
| A. | 7π | B. | 9π | C. | 11π | D. | 13π |