题目内容
18.函数f(x)=$\left\{\begin{array}{l}{0,x∈\{0,4\}}\\{{x}^{2}-2x+3,0<x≤2}\\{|x-3|,2<x<4}\end{array}\right.$,若f(x)=kx有三个不同的根,则实数k的取值范围是( )| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
分析 作出f(x)与y=kx的函数图象,根据交点个数判断k的范围.
解答 解:作出f(x)与y=kx的函数图象如图所示: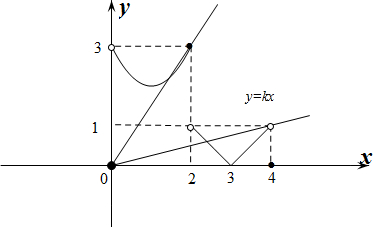
若直线y=kx过(4,1),则k=$\frac{1}{4}$,
若直线y=kx过(2,3),则k=$\frac{3}{2}$,
若直线y=kx与y=x2-2x+3相切,设切点坐标为(x0,y0),
则$\left\{\begin{array}{l}{{y}_{0}=k{x}_{0}}\\{{y}_{0}={{x}_{0}}^{2}-2{x}_{0}+3}\\{2{x}_{0}-2=k}\end{array}\right.$,解得x0=$\sqrt{3}$,y0=6-2$\sqrt{3}$,k=2$\sqrt{3}$-2,
∴当0≤k<$\frac{1}{4}$或2$\sqrt{3}-2$<k≤$\frac{3}{2}$时,直线y=kx与f(x)的图象有3个交点,
故选B.
点评 本题考查了方程解与函数图象的关系,导数的几何意义,属于中档题.

练习册系列答案
相关题目
13.已知O(0,0),A(-1,3),B(2,-4),$\overrightarrow{OP}$=2$\overrightarrow{OA}$+m$\overrightarrow{AB}$,若点P在y轴上,则m=( )
| A. | $\frac{2}{3}$ | B. | $\frac{6}{7}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{6}{7}$ |
12.已知二面角α-AB-β的平面角是锐角θ,α内一点C到β的距离为3,点C到棱AB的距离为4,那么cosθ的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $\frac{\sqrt{7}}{4}$ |
10.定义在实数域上的偶函数f(x)对于?x∈R,均满足条件f(x+2)=f(x)+f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上恰有4个零点,则a的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
7.将函数y=cos(2x+$\frac{π}{6}$)图象上的点P($\frac{π}{4}$,t)向右平移m(m>0)个单位长度得到点P1,若P1位于函数y=cos2x的图象上,则( )
| A. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{6}$ | B. | t=-$\frac{\sqrt{3}}{2}$,m的最小值为$\frac{π}{12}$ | ||
| C. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{12}$ | D. | t=-$\frac{1}{2}$,m的最小值为$\frac{π}{6}$ |
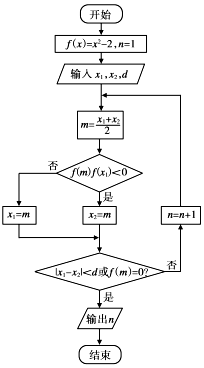 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )