题目内容
13.已知O(0,0),A(-1,3),B(2,-4),$\overrightarrow{OP}$=2$\overrightarrow{OA}$+m$\overrightarrow{AB}$,若点P在y轴上,则m=( )| A. | $\frac{2}{3}$ | B. | $\frac{6}{7}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{6}{7}$ |
分析 根据题意,由O、A、B的坐标计算可得$\overrightarrow{OA}$、$\overrightarrow{AB}$的坐标,进而可得$\overrightarrow{OP}$=2$\overrightarrow{OA}$+m$\overrightarrow{AB}$=(-2+3m,6-7m),结合题意,若点P在y轴上,则-2+3m=0,解可得m的值,即可得答案.
解答 解:根据题意,O(0,0),A(-1,3),B(2,-4),
则$\overrightarrow{OA}$=(-1,3),$\overrightarrow{AB}$=(3,-7),
则$\overrightarrow{OP}$=2$\overrightarrow{OA}$+m$\overrightarrow{AB}$=(-2+3m,6-7m),
若点P在y轴上,则-2+3m=0,解可得m=$\frac{2}{3}$;
故选:A.
点评 本题考查平面向量的坐标运算,关键是求出$\overrightarrow{OP}$的坐标.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
5.函数y=xex的导数是( )
| A. | y=xex | B. | y=x+xex | C. | y=ex | D. | y=(1+x)ex |
5.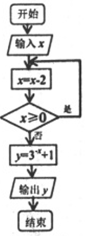 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )
 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )| A. | $\frac{4}{3}$ | B. | 10 | C. | 4 | D. | 2 |
2.平面内三个向量$\overrightarrow{{a}_{i}}$(i=1,2,3)满足$\overrightarrow{{a}_{1}}$⊥$\overrightarrow{{a}_{2}}$,|$\overrightarrow{{a}_{i}}$-$\overrightarrow{{a}_{i+1}}$|=1(规定$\overrightarrow{{a}_{4}}$=$\overrightarrow{{a}_{1}}$),则( )
| A. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=0 | B. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)min=-1 | C. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{3}{4}$ | D. | ($\overrightarrow{{a}_{i}}$•$\overrightarrow{{a}_{i+1}}$)max=$\frac{2}{3}$ |
18.函数f(x)=$\left\{\begin{array}{l}{0,x∈\{0,4\}}\\{{x}^{2}-2x+3,0<x≤2}\\{|x-3|,2<x<4}\end{array}\right.$,若f(x)=kx有三个不同的根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |