题目内容
4.学生在野营活动中,用直杆搭建一个支架进行野炊,如图1所示,已知PA=PB=PC=140cm,点C到A、B两点的距离相等,E、F、G、H分别是PA、PB、PC、EF的中点,直杆GH与底面ABC的距离为50cm.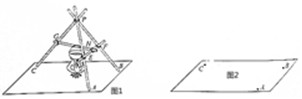
(1)在图2中画出相应于图1的空间图形;三棱锥P-ABC及相关线段EF、GH;
(2)求PC与底面ABC所成角的大小(结果用反三角形式表示);
(3)判断PC与EF是否互相垂直,并说明理由.
分析 (1)根据条件作图;
(2)求出P到平面ABC的距离,则利用三角函数定义得出线面角的正弦值;
(3)取AB中点M,连结CM,PM,证明AB⊥平面PCM,EF∥AB即可得出结论.
解答 解:(1)作出空间图形如下: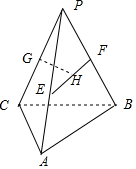
(2)过P作PO⊥平面ABC,垂足为O,连结OC,
则∠PCO为PC与平面ABC所成的角.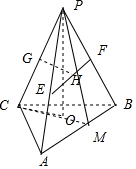
∵GH∥平面ABC,GH到平面ABC的距离为50,G是PC的中点,
∴P到平面ABC的距离为100,即PO=100,
∴sin∠PCO=$\frac{PO}{PC}=\frac{5}{7}$,
∴∠PCO=arcsin$\frac{5}{7}$.
(3)取AB中点M,连结CM,PM,
∵PA=PB,CA=CB,M是AB的中点,
∴CM⊥AB,PM⊥AB,
又PM∩CM=M,
∴AB⊥平面PCM,又PC?平面PCM,
∴AB⊥PC,
∵E,F是PA,PB的中点,
∴EF∥AB,
∴PC⊥EF.
点评 本题考查了线面垂直的判定,线面角的计算,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.函数f(x)=$\left\{\begin{array}{l}{0,x∈\{0,4\}}\\{{x}^{2}-2x+3,0<x≤2}\\{|x-3|,2<x<4}\end{array}\right.$,若f(x)=kx有三个不同的根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
16.在拍毕业照时,六个同学排成一排照相,要求其中一对好友甲和乙相邻,且同学丙不能和甲相邻的概率为( )
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
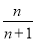 ,则
,则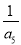 等于( )
等于( )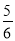 B.
B.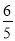 C.
C.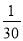 D.30
D.30 内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )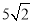 B.
B.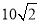 C.
C.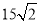 D.
D.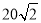
 ,则
,则 ”的否命题是( )
”的否命题是( )
 ,则
,则
 ,则
,则