题目内容
1.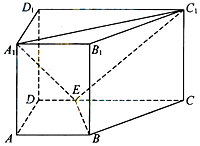 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1-EA1C1的体积.
分析 (1)过B作CD的垂线交CD于F,推导出BE⊥BC,BE⊥BB1,由此能证明BE⊥平面BB1C1C.
(2)三棱锥B1-EA1C1的体积:${V}_{{B}_{1}-E{A}_{1}{C}_{1}}$=${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$,由此能求出结果.
解答 证明:(1)过B作CD的垂线交CD于F,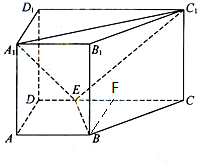
则$BF=AD=\sqrt{2},EF=AB-DE=1,FC=2$
在$Rt△BFE中,BE=\sqrt{3},Rt△BFC中,BC=\sqrt{6}$.
在△BCE中,∵BE2+BC2=9=EC2,
∴BE⊥BC,∵BB1⊥平面ABCD,∴BE⊥BB1,
∵BC∩BB1=B,∴BE⊥平面BB1C1C,
(2)∵点E到平面A11C1的距离为AA1=3,
∴三棱锥B1-EA1C1的体积:
${V}_{{B}_{1}-E{A}_{1}{C}_{1}}$=${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}×A{A}_{1}×{S}_{△{A}_{1}{B}_{1}{C}_{1}}$
=$\frac{1}{3}×3×[\frac{1}{2}×(2+4)×\sqrt{2}-\frac{1}{2}×4×\sqrt{2}]$=$\sqrt{2}$.
点评 本题考查线面垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
13.已知向量$\overrightarrow{OA}=(1,-3),\overrightarrow{OB}=(2,-1),\overrightarrow{OC}=(k+1,k-2)$,若A、B、C三点共线,则实数k应满足的条件是( )
| A. | k=-2 | B. | $k=\frac{1}{2}$ | C. | k=1 | D. | k=-1 |
9.甲、乙两艘货轮都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随即到达,则两船中有一艘在停泊位时,另一艘船必须等待的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
13.已知函数f(x)=cosx,若存在实数x1,x2,…,xm(m≥2,m∈N)满足条件0≤x1<x2<…<xm≤6π,且|f(x1)-f(x2)|+…+|f(xm-1)-f(xm)|=12,则m的最小值为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
10.设z1,z2是复数,则下列结论中正确的是( )
| A. | 若${z_1}^2+{z_2}^2>0$,则 ${z_1}^2>-{z_2}^2$ | |
| B. | $|{{z_1}-{z_2}}|=\sqrt{{z_1}^2+{z_2}^2-4{z_1}{z_2}}$ | |
| C. | ${z_1}^2+{z_2}^2=0?{z_1}={z_2}$ | |
| D. | |z1|2=|$\overline{{z}_{1}}$|2 |
 满足
满足 ,则
,则 的最大值为
的最大值为 B.
B. C.1 D.
C.1 D.