题目内容
6.已知函数f(x)=|x-1|-|x+2|.(Ⅰ)求不等式-2<f(x)<0的解集A;
(Ⅱ)若m,n∈A,证明:|1-4mn|>2|m-n|.
分析 (Ⅰ)根据f(x)的解析式,求得不等式-2<f(x)<0的解集A.
(Ⅱ)由(Ⅰ)可知,${m^2}<\frac{1}{4},{n^2}<\frac{1}{4}$,故要证明|1-4mn|>2|m-n|,只要证明左边的平方大于右边的平方即可.
解答 解:(Ⅰ)依题意,$f(x)=|{x-1}|-|{x+2}|=\left\{\begin{array}{l}3,x≤-2\\-2x-1,-2<x<1\\-3,x≥1\end{array}\right.$,
由不等式-2<f(x)<0,可得-2<-2x-1<0,解得$-\frac{1}{2}<x<\frac{1}{2}$,故$A=(-\frac{1}{2},\frac{1}{2})$.
(Ⅱ)由(Ⅰ)可知,${m^2}<\frac{1}{4},{n^2}<\frac{1}{4}$;
因为|1-4mn|2-4|m-n|2=(1-8mn+16m2n2)-4(m2-2mn+n2)=(4m2-1)(4n2-1)>0,
故|1-4mn|2>4|m-n|2,故|1-4mn|>2|m-n|.
点评 本题主要考查带有绝对值的函数,绝对值不等式的解法,证明不等式的方法,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
17.已知$\frac{{{a^2}+2a+2}}{x}≤$$\frac{4}{{{x^2}-x}}+1$对于任意的x∈(1,+∞)恒成立,则( )
| A. | a的最小值为-3 | B. | a的最小值为-4 | C. | a的最大值为2 | D. | a的最大值为4 |
14.设$0<α<β<\frac{π}{2},sinα=\frac{3}{5},cos(β-α)=\frac{12}{13}$,则sinβ的值为( )
| A. | $\frac{16}{65}$ | B. | $\frac{33}{65}$ | C. | $\frac{56}{65}$ | D. | $\frac{63}{65}$ |
11.已知数列{an}前n项和为${S_n}={n^2}-2n+a$,若该数列是等差数列,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 不确定 |
18.已知点A(0,-1)是抛物线C:x2=2py(p>0)准线上的一点,点F是抛物线C的焦点,点P在抛物线C上且满足|PF|=m|PA|,当m取最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
15.命题甲:f(x)在区间(a,b)内递增;命题乙:对任意x∈(a,b),有f'(x)>0.则甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

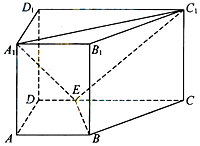 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3