题目内容
已知函数f(x)=
(k∈R).若函数y=|f(x)|+k有三个零点,则实数k的取值范围是( )
|
| A、k≤-2 |
| B、-2≤k<-1 |
| C、-1<k<0 |
| D、k≤2 |
考点:函数零点的判定定理,函数的图象
专题:计算题,函数的性质及应用
分析:函数y=|f(x)|+k有三个零点可化为方程|f(x)|=-k有三个不同的解,则k<0,此时|lnx|=-k有两个解,则|kx+2|=-k在(-∞,0]只有一个解,从而求出实数k的取值范围.
解答:
解:函数y=|f(x)|+k有三个零点可化为方程|f(x)|=-k有三个不同的解,
若k=0,则x=1,只有一个解,不成立,则k<0;
若|lnx|=-k,则x=ek或x=e-k,
则|kx+2|=-k在(-∞,0]只有一个解,
在(-∞,0]上,|kx+2|=kx+2=-k,
则x=
≤0,则k≤-2,
故选A.
若k=0,则x=1,只有一个解,不成立,则k<0;
若|lnx|=-k,则x=ek或x=e-k,
则|kx+2|=-k在(-∞,0]只有一个解,
在(-∞,0]上,|kx+2|=kx+2=-k,
则x=
| -k-2 |
| k |
故选A.
点评:本题考查了函数的零点与方程的根之间的关系,本题将函数的零点化为了方程的根,同时才查了化简的技巧,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
某企业近几年的年产值如图,则年增长率最高的是( )(年增长率=年增长值/年产值)

| A、97年 | B、98年 |
| C、99年 | D、00年 |
设函数f(x)=
=x(a∈R)在[-1,1]上有解,则a的取值范围是( )
| 2x+x-a |
| A、[1,2] | ||
B、[-
| ||
| C、[1,3] | ||
D、[-
|
已知A,B,C三点不共线,空间内任一点O满足
=x
+y
+z
(x,y,z∈R),则“x+y+z=1”是“点P在由A,B,C所确定的平面内”的( )
| OP |
| OA |
| OB |
| OC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
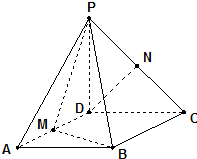 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.