题目内容
9．一箱内有十张标有0到9的卡片，从中任选一张，则取到卡片上的数字不小于6的概率是$\frac{2}{5}$．分析 先求出基本事件总数n=10，取到卡片上的数字不小于6包含的基本事件个数m=4，由此能求出取到卡片上的数字不小于6的概率．
解答 解：一箱内有十张标有0到9的卡片，从中任选一张，
基本事件总数n=10，
取到卡片上的数字不小于6包含的基本事件个数m=4，
∴取到卡片上的数字不小于6的概率是p=$\frac{m}{n}=\frac{4}{10}=\frac{2}{5}$．
故答案为：$\frac{2}{5}$．
点评 本题考查等可能事件概率计算公式、古典概型等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．
练习册系列答案
相关题目
20．某连锁经营公司所属个零售店某月的销售额和利润额资料如表：
（1）用最小二乘法计算利润额对销售额y的回归直线方程；
（2）当销售额为4（千万元）时，估计利润额的大小．
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$．
| 商店名称 | A | B | C | D | E |
| 销售额x（千万元） | 3 | 5 | 6 | 7 | 9 |
| 利润率y（千万元） | 2 | 3 | 3 | 4 | 5 |
（2）当销售额为4（千万元）时，估计利润额的大小．
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$．
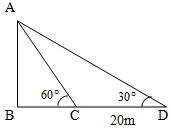如图所示，为测量一水塔AB的高度，在C处测得塔顶的仰角为60°，后退20米到达D处测得塔顶的仰角为30°，则水塔的高度为$10\sqrt{3}$米．
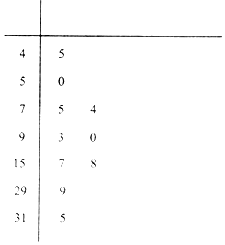近年来，空气质量成为人们越来越关注的话题，空气质量指数（AirQualityIndex，简称AQI）是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级，0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；大于300为严重污染．环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下：