题目内容
14.在△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{cosB-2cosA}{cosC}$=$\frac{2a-b}{c}$(Ⅰ)若b=2,求a的值;
(Ⅱ)若角A是钝角,且c=3,求b的取值范围.
分析 (Ⅰ)把已知等式利用正弦定理化边为角,结合两角和的正弦可得sin(B+C)=2sin(A+C).进一步得到sinA=2sinB,可得a=2b.则答案可求;
(Ⅱ)利用余弦定理结合a=2b可得b>$\sqrt{3}$.再由两边之和大于第三边可得b<3.
解答 解:(Ⅰ)由题意及正弦定理,得$\frac{cosB-2cosA}{cosC}=\frac{2sinA-sinB}{sinC}$,
即sinCcosB-2sinCcosA=2sinAcosC-sinBcosC,
则sinCcosB+sinBcosC=2(sinCcosA+sinAcosC),
∴sin(B+C)=2sin(A+C).
∵△ABC中,A+B+C=π,
∴sinA=2sinB,故a=2b.
由b=2,得a=4;
(Ⅱ)由(Ⅰ)可知,a=2b,由余弦定理可得:
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{{b}^{2}+9-4{b}^{2}}{6b}=\frac{9-3{b}^{2}}{6b}$<0,
则b>$\sqrt{3}$.
在△ABC中,b+c>a,即b+3>2b,则b<3.
∴b的取值范围为($\sqrt{3},3$).
点评 本题考查三角形的解法,考查余弦定理及正弦定理在解三角形中的应用,是中档题.

练习册系列答案
相关题目
5.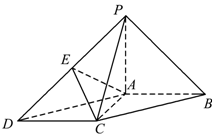 如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.
如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.
(1)求证:PB∥平面AEC;
(2)求二面角E-AC-B的大小.
 如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.
如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.(1)求证:PB∥平面AEC;
(2)求二面角E-AC-B的大小.
2.已知向量$\overrightarrow a$,$\overrightarrow b$不共线,且对任意实数x,不等式$|{\overrightarrow a-x\overrightarrow b}|≥|{\overrightarrow a-\overrightarrow b}|$恒成立,则下列结论一定成立的是( )
| A. | $\overrightarrow a$•$\overrightarrow b$-${\overrightarrow b^2}$=0 | B. | ${\overrightarrow a^2}-\overrightarrow a$•$\overrightarrow b$=0 | C. | $\overrightarrow a$⊥$\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
19.在区间[0,4]上随机产生两个均匀随机数分别赋给a,b,则|a-b|≤1的概率为( )
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{23}{32}$ |
4.二项式(x+1)n(n∈N+)的展开式中x2与x4系数相同,则n=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 7 |