题目内容
19.设向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(cosx,cosx),x∈R,函数f(x)=$\overrightarrow{a}$•($\overrightarrow{a}+\overrightarrow{b}$)(1)求函数f(x)的最大值;
(2)求函数f(x)在[0,π]上的单调增区间.
分析 (1)根据平面向量的数量积运算与三角恒等变换,求出函数f(x)的最大值;
(2)利用正弦函数的图象与性质,求出f(x)在[0,π]上的单调增区间.
解答 解 (1)∵向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(cosx,cosx),
∴函数f(x)=$\overrightarrow{a}$•($\overrightarrow{a}+\overrightarrow{b}$)
=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$$•\overrightarrow{b}$
=sin2x+cos2x+sinxcosx+cos2x
=1+$\frac{1}{2}$sin2x+$\frac{1}{2}$(1+cos2x)
=$\frac{3}{2}$+$\frac{1}{2}$(sin2x+cos2x)
=$\frac{3}{2}$+$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$),
∴函数f(x)的最大值是$\frac{3}{2}+\frac{{\sqrt{2}}}{2}$;…(6分)
(2)∵f(x)=$\frac{3}{2}$+$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$),
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2x+$\frac{π}{2}$,k∈Z,…(9分)
解得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,k∈Z;
∴函数在[0,π]上的单调增区间为[0,$\frac{π}{8}$]和[$\frac{5π}{8}$,π]…(12分)
点评 本题考查了三角恒等变换与平面向量的数量积应用问题,也考查了三角函数的图象与性质的应用问题,是综合题.

| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 售量y | 11 | 10 | 8 | 6 | 5 |
在2013春节间市价部门,对本五商场销售的某商天的销售及其价格进行调查,五个商场的售价x元和销量件之的一组数据表所示:欲销售量为12,价格应定为少.
附:在回归直线y=$\widehat{b}$x+$\widehat{a}$中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$.
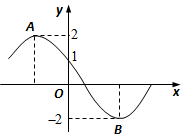 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=2.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=2.