题目内容
17．若复数z=（a2-4）+（a+2）i为纯虚数，则复数$\frac{a+i}{1-i}$在复平面上对应的点位于第一象限．分析 利用复数的运算法则、纯虚数的定义、几何意义即可得出．
解答 解：z=（a2-4）+（a+2）i为纯虚数，∴a2-4=0，a+2≠0．解得a=2．
则复数$\frac{a+i}{1-i}$=$\frac{2+i}{1-i}$=$\frac{（2+i）（1+i）}{（1-i）（1+i）}$=$\frac{1}{2}+\frac{3}{2}$i在复平面上对应的点$（\frac{1}{2}，\frac{3}{2}）$位于第 一象限．
故答案为：一．
点评 本题考查了复数的运算法则、纯虚数的定义、几何意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
7．
经过分析，发现售量y对商的价格x具有线性相关系．
在2013春节间市价部门，对本五商场销售的某商天的销售及其价格进行调查，五个商场的售价x元和销量件之的一组数据表所示：欲销售量为12，价格应定为少．
附：在回归直线y=$\widehat{b}$x+$\widehat{a}$中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$．
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 售量y | 11 | 10 | 8 | 6 | 5 |
在2013春节间市价部门，对本五商场销售的某商天的销售及其价格进行调查，五个商场的售价x元和销量件之的一组数据表所示：欲销售量为12，价格应定为少．
附：在回归直线y=$\widehat{b}$x+$\widehat{a}$中$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$．
5．
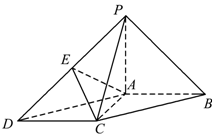如图所示，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且 PA=AB=2，AC=1，点E是PD的中点．
（1）求证：PB∥平面AEC；
（2）求二面角E-AC-B的大小．
如图所示，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且 PA=AB=2，AC=1，点E是PD的中点．（1）求证：PB∥平面AEC；
（2）求二面角E-AC-B的大小．
12．已知三点坐标A（0，-4），B（4，0），C（-6，2），点D，E，F分别为线段BC，CA，AB的中点，则直线EF的方程为（ ）
| A． | x+5y+8=0 | B． | x-y+2=0 | C． | x+y=0 | D． | x+y+4=0 |
2．已知向量$\overrightarrow a$，$\overrightarrow b$不共线，且对任意实数x，不等式$|{\overrightarrow a-x\overrightarrow b}|≥|{\overrightarrow a-\overrightarrow b}|$恒成立，则下列结论一定成立的是（ ）
| A． | $\overrightarrow a$•$\overrightarrow b$-${\overrightarrow b^2}$=0 | B． | ${\overrightarrow a^2}-\overrightarrow a$•$\overrightarrow b$=0 | C． | $\overrightarrow a$⊥$\overrightarrow b$ | D． | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
7．已知圆A：x2+y2=1在伸缩变换$\left\{{\begin{array}{l}{x'=2x}\\{y'=3y}\end{array}}\right.$的作用下变成曲线C，则曲线C的方程为（ ）
| A． | 2x2+3y2=1 | B． | 4x2+9y2=1 | C． | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | D． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 |