题目内容
有下列说法:
(1)函数y=-cos2x的最小正周期是π;
(2)终边在y轴上的角的集合是{α|α=
,k∈Z};
(3)函数y=4sin(2x-
)的一个对称中心为(
,0)
(4)设△ABC是锐角三角形,则点P(sinA-cosB,cos(A+B))在第四象限
则正确命题的序号是 .
(1)函数y=-cos2x的最小正周期是π;
(2)终边在y轴上的角的集合是{α|α=
| kπ |
| 2 |
(3)函数y=4sin(2x-
| π |
| 3 |
| π |
| 6 |
(4)设△ABC是锐角三角形,则点P(sinA-cosB,cos(A+B))在第四象限
则正确命题的序号是
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由条件利用余弦函数的图象和性质,判断各个选项是否正确,从个人得出结论.
解答:
解:由于函数y=-cos2x的最小正周期是
=π,故(1)正确.
由于终边在y轴上的角的集合是{α|α=kπ+
=
,k∈Z},故(2)不正确.
由于x=
时函数y=4sin(2x-
)=0,可得函数y=4sin(2x-
)的一个对称中心为(
,0),
故(3)正确.
由于△ABC是锐角三角形,则A+B>
,即 A>
-B>0,∴sinA>sin(
-B)=cosB,
∴sinA-cosB>0,cos(A+B)<0,
故点P(sinA-cosB,cos(A+B))在第四象限,故(4)正确.
故答案为:(1)、(3)、(4).
| 2π |
| 2 |
由于终边在y轴上的角的集合是{α|α=kπ+
| π |
| 2 |
| (2k+1)π |
| 2 |
由于x=
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
故(3)正确.
由于△ABC是锐角三角形,则A+B>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴sinA-cosB>0,cos(A+B)<0,
故点P(sinA-cosB,cos(A+B))在第四象限,故(4)正确.
故答案为:(1)、(3)、(4).
点评:本题主要考查余弦函数的图象和性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.下列各对事件中,为对立事件的是( )
| A、恰有一名男生和恰有2名男生 |
| B、至少一名男生和至少一名女生 |
| C、至少有一名男生和与全是女生 |
| D、至少有一名男生和全是男生 |
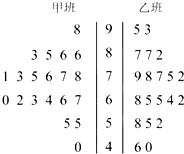 某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.
某次月考从甲、乙两班中各抽取20个物理成绩,整理数据得到茎叶图如图所示,根据茎叶图解决下列问题.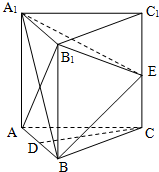 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.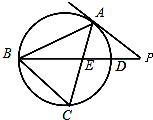 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=