题目内容
19.若△ABC中,AC=$\sqrt{6}$,A=45°,C=75°,则BC=2.分析 由已知可求B的值,利用正弦定理即可求BC的值.
解答 解:∵AC=$\sqrt{6}$,A=45°,C=75°,
∴B=π-A-C=60°,
∴由正弦定理可得:BC=$\frac{ACsinA}{sinB}$=$\frac{\sqrt{6}×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=2.
故答案为:2.
点评 本题主要考查了三角形内角和定理,正弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
9.如果f(x)在[-5,5]上是奇函数,且f(3)<f(1),则( )
| A. | f(-1)<f(-3) | B. | f(0)>f(1) | C. | f(-1)<f(1) | D. | f(-3)<f(-5) |
7.下列关于函数f(x)=sinx(cosx+sinx)的说法中,不正确的是( )
| A. | f(x)的最小正周期为π | |
| B. | f(x)的图象关于直线x=-$\frac{π}{8}$对称 | |
| C. | f(x)的图象关于点($\frac{π}{8}$,0)对称 | |
| D. | f(x)的图象向右平移$\frac{π}{8}$后得到一个偶函数的图象 |
11.已知关于x的二次函数f(x)=ax2-4bx+1,设集合A={-1,1,2,3,4,5},B={-2,-1,1,2,3,4},分别从集合A和B中随机取一个数记为a和b,则函数y=f(x)在[1,+∞)上单调递增的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
9.已知函数f(x)=x2+a(b+1)x+a+b(a,b∈R),则“a=0”是“f(x)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
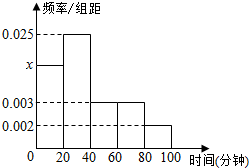 某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动