题目内容
19. 如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.
如图,在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q.(1)求证:PQ∥平面ABC1;
(2)若AB=AA1,BC=3,AC1=3,BC1=$\sqrt{13}$,求证:平面ABC1⊥平面AA1C1C.
分析 (1)在BB1取点E,使BE=3EB1,连结PE、QE,推导出平面ABC1∥平面PQE,由此能证明PQ∥平面ABC1.
(2)推导出AB⊥CC1,BC⊥CC1,AB⊥AC,从而AB⊥平面AA1C1C,由此能证明平面ABC1⊥平面AA1C1C.
解答 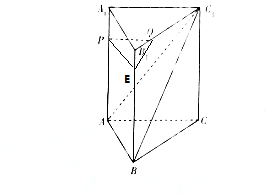 证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
证明:(1)在BB1取点E,使BE=3EB1,连结PE、QE,
∵在直三棱柱ABC-A1B1C1中,P,Q分别是AA1,B1C1上的点,且AP=3A1P,B1C1=4B1Q,
∴PE∥AB,QE∥BC1,
∵AB∩BC1=B,PE∩QE=E,AB、BC1?平面ABC1,
PE、QE?平面PQE,
∴平面ABC1∥平面PQE,
∵PQ?平面PQE,∴PQ∥平面ABC1.
解:(2)∵在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,
∴AB⊥CC1,BC⊥CC1,
∵AB=AA1,BC=3,AC1=3,BC1=$\sqrt{13}$,
∴AB=AA1=CC1=$\sqrt{13-9}$=2,AC=$\sqrt{A{{C}_{1}}^{2}-C{{C}_{1}}^{2}}$=$\sqrt{9-4}$=$\sqrt{5}$,
∴AB2+AC2=BC2,∴AB⊥AC,
又AC∩CC1=C,∴AB⊥平面AA1C1C,
∵AB?平面ABC1,∴平面ABC1⊥平面AA1C1C.
点评 本题考查线面平行、面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.如图所示的程序框图,若输入n,x的值分别为3,3,则输出v的值为( )


| A. | 1 | B. | 5 | C. | 16 | D. | 48 |
8.已知复数z1=3+ai,z2=a-3i(i为虚数单位),若z1•z2是实数,则实数a的值为( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
9.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)的图象与x轴交点的横坐标,依次构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象,则( )
| A. | g(x)是奇函数 | B. | g(x)的图象关于直线x=-$\frac{π}{4}$对称 | ||
| C. | g(x)在[$\frac{π}{4}$,$\frac{π}{2}$]上的增函数 | D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,g(x)的值域是[-2,1] |
 如图,点M($\sqrt{3}$,$\sqrt{2}$)在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且点M到两焦点的距离之和为6.
如图,点M($\sqrt{3}$,$\sqrt{2}$)在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,且点M到两焦点的距离之和为6.