题目内容
设数列{an}的首项为m,公比为q(q≠1)的等比数列,Sn是它的前n项的和,对任意的n∈N*,点(an,
)在直线( )上.
| S2n |
| Sn |
| A、qx+my-q=0 |
| B、qx-my+m=0 |
| C、mx+qy-q=0 |
| D、qx+my+m=0 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用等比数列的通项与求和公式,求出an=mqn-1,Sn=
,可得
=1+qn,代入验证即可得出结论.
| m(1-qn) |
| 1-q |
| S2n |
| Sn |
解答:
解:∵数列{an}的首项为m,公比为q(q≠1)的等比数列,
∴an=mqn-1,Sn=
,
∴
=1+qn,
∴q•=mqn-1-m(1+qn)+m=0,
∴点(an,
)在直线qx-my+m=0上.
故选:B.
∴an=mqn-1,Sn=
| m(1-qn) |
| 1-q |
∴
| S2n |
| Sn |
∴q•=mqn-1-m(1+qn)+m=0,
∴点(an,
| S2n |
| Sn |
故选:B.
点评:本题考查等比数列的通项与求和公式,考查数列的函数性质,属于基础题.

练习册系列答案
相关题目
设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=( )
| A、0 | B、1 | C、2 | D、3 |
函数f(x)=
的定义域为( )
| 1 | ||
|
A、(0,
| ||
| B、(2,+∞) | ||
C、(0,
| ||
D、(0,
|
如图所示,程序框图(算法流程图)的输出结果是( )
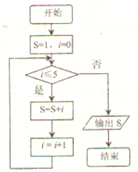

| A、11 | B、15 | C、16 | D、22 |
一几何体的直观图如图所示,下列给出的四个俯视图中正确的是( )


A、 |
B、 |
C、 |
D、 |
已知四棱锥P-ABCD,现要在四棱锥的各个面上涂色,有4种不同的颜色可供选择,要求相邻的面不同色,则不同的涂色方法有( )种.
| A、60 | B、120 | C、48 | D、72 |