题目内容
9.点E,F分别是正方形ABCD的边AB和CD上的点且AB=2AE,CD=4FD,点P为线段EF上的动点$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则$\frac{1}{x}$+$\frac{1}{y}$的最小值为$\frac{9}{2}$.分析 用$\overrightarrow{AE},\overrightarrow{AF}$表示出$\overrightarrow{AP}$,利用三点共线原理得出x,y的关系,使用基本不等式得出最小值.
解答 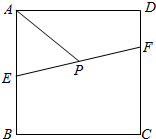 解:∵AB=2AE,CD=4FD,∴$\overrightarrow{AB}=2\overrightarrow{AE}$,$\overrightarrow{DF}$=$\frac{1}{4}\overrightarrow{DC}=\frac{1}{4}\overrightarrow{AB}$,
解:∵AB=2AE,CD=4FD,∴$\overrightarrow{AB}=2\overrightarrow{AE}$,$\overrightarrow{DF}$=$\frac{1}{4}\overrightarrow{DC}=\frac{1}{4}\overrightarrow{AB}$,
∴$\overrightarrow{AD}=\overrightarrow{AF}-\overrightarrow{DF}$=$\overrightarrow{AF}-\frac{1}{4}\overrightarrow{AB}$=$\overrightarrow{AF}-\frac{1}{2}\overrightarrow{AE}$,
∴$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$=2x$\overrightarrow{AE}$+y($\overrightarrow{AF}-\frac{1}{2}\overrightarrow{AE}$)=(2x-$\frac{y}{2}$)$\overrightarrow{AE}$+y$\overrightarrow{AF}$.
∵E,F,P三点共线,∴2x-$\frac{y}{2}$+y=1,即2x+$\frac{y}{2}$=1.
∴$\frac{1}{x}$+$\frac{1}{y}$=$\frac{2x+\frac{y}{2}}{x}$+$\frac{2x+\frac{y}{2}}{y}$=$\frac{y}{2x}$+$\frac{2x}{y}$+$\frac{5}{2}$≥2+$\frac{5}{2}$=$\frac{9}{2}$.
故答案为$\frac{9}{2}$.
点评 本题考查了平面向量的基本定理,基本不等式的应用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -3 | B. | $-\frac{3}{5}$ | C. | $-\frac{1}{3}$ | D. | 1 |
| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
| A. | (0,+∞) | B. | (5,+∞) | C. | (8,+∞) | D. | (-∞,+∞) |
| A. | k>0或k≤-9 | B. | k≥1 | C. | -9≤k≤1 | D. | 0≤k≤1 |
| A. | (-∞,0)∪(1,2) | B. | [0,+∞) | C. | (-∞,1]∪[2,+∞) | D. | [0,1]∪[2,+∞) |