题目内容
已知正方体ABCD-A′B′C′D′的棱长为1，设
=
，
=
，
=
，则|
+
+
|= ．
| AB |
| a |
| AD |
| b |
| AA′ |
| c |
| a |
| b |
| 1 |
| 2 |
| c |
考点：空间向量的夹角与距离求解公式,空间向量的数量积运算
专题：空间向量及应用
分析：取CC1中点E，连结AC，AE，结合正方体的结构特征，利用向量加法三角形法则得到
+
+
=
+
+
=
，再利用勾股定理能求出|
+
+
|的值．
| a |
| b |
| 1 |
| 2 |
| c |
| AB |
| BC |
| CE |
| AE |
| a |
| b |
| 1 |
| 2 |
| c |
解答：
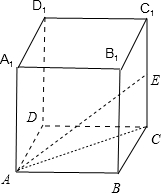解：取CC1中点E，连结AC，AE，
∵正方体ABCD-A′B′C′D′的棱长为1，
设
=
，
=
，
=
，
则
+
+
=
+
+
=
，
∴|
+
+
|=|
|=
=
=
．
故答案为：
．
解：取CC1中点E，连结AC，AE，∵正方体ABCD-A′B′C′D′的棱长为1，
设
| AB |
| a |
| AD |
| b |
| AA′ |
| c |
则
| a |
| b |
| 1 |
| 2 |
| c |
| AB |
| BC |
| CE |
| AE |
∴|
| a |
| b |
| 1 |
| 2 |
| c |
| AE |
| AC2+CE2 |
(12+12)+(
|
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查向量和的模的求法，是基础题，解题时要注意空间向量加法的三角形法则的合理运用．
练习册系列答案
名校通行证有效作业系列答案
相关题目
若等比数列{an}的各项均为正数，且a10a11+a9a12=2e5，则lna1+lna2+…+lna20等于（ ）
| A、50 | B、25 | C、75 | D、100 |
设l，m是两条不同的直线，α，β是不同的平面，则下列命题正确的是（ ）
| A、若l⊥m，m?α，则l⊥α |
| B、若l∥α，m?α，则l∥m |
| C、若α∥β，l?α，则l∥β |
| D、若α⊥β，l?α，则l⊥β |
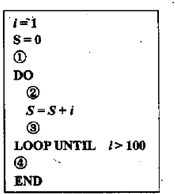如图的语句是求S=1+2+3+…+100的一个程序，语句i=i+1应当在这个程序中的①②③④四处的哪一处才能实现上述功能（ ）