题目内容
设l,m是两条不同的直线,α,β是不同的平面,则下列命题正确的是( )
| A、若l⊥m,m?α,则l⊥α |
| B、若l∥α,m?α,则l∥m |
| C、若α∥β,l?α,则l∥β |
| D、若α⊥β,l?α,则l⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面垂直、线面平行、面面平行、面面垂直的性质定理和判定定理对选项分别分析选择.
解答:
解:对于A,若l⊥m,m?α,则l可能在α;故A错误;
对于B,若l∥α,m?α,则l与m的位置关系是平行或者异面;故B错误;
对于C,若α∥β,l?α,根据面面平行的性质可得l∥β;故C正确;
对于D,若α⊥β,l?α,则l与β可能平行或者相交;故D错误;
故选C.
对于B,若l∥α,m?α,则l与m的位置关系是平行或者异面;故B错误;
对于C,若α∥β,l?α,根据面面平行的性质可得l∥β;故C正确;
对于D,若α⊥β,l?α,则l与β可能平行或者相交;故D错误;
故选C.
点评:本题考查了线面垂直、线面平行、面面平行、面面垂直的性质定理和判定定理,熟练掌握相关的定理是解答的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在某市2014年6月的高二质量检测考试中,理科学生的数学成绩服从正态分布N(98,100).已知参加本次考试的全市理科学生约9 450人.某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第( )名?
(参考数值:P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974)
(参考数值:P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974)
| A、1 500 |
| B、1 700 |
| C、4 500 |
| D、8 000 |
已知l,m,n是三条不同的直线,α,β,γ是三个不同的平面,下面命题正确的是( )
| A、若m⊥l,n⊥l,则m∥n |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若m∥l,n∥l,则m∥n |
| D、若m∥α,n∥α,则m∥n |
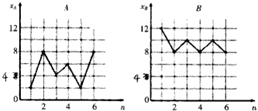 如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为
如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为. |
| xA |
. |
| xB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

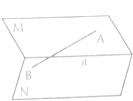 二面角M-a-N中,点A∈M,点B∈N,AB=4
二面角M-a-N中,点A∈M,点B∈N,AB=4