题目内容
若f（x）为定义在R上的奇函数，当x＞0时，f（x）=sin2x+cosx，则f（x）的解析式为 ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由奇函数的性质可得：f（0）=0，再设x＜0则-x＞0，利用题意和奇函数的性质求出x＜0时的解析式，再用分段函数的形式表示出函数的解析式．
解答：
解：因为f（x）为定义在R上的奇函数，所以f（0）=0，
设x＜0，则-x＞0，因为当，时，f（x）=sin2x+cosx，
所以f（-x）=sin（-2x）+cos（-x）=-sin2x+cosx，
因为f（x）为定义在R上的奇函数，
所以f（x）=-f（-x）=sin2x-cosx，
综上得，f(x)=
，
故答案为：f(x)=
．
设x＜0，则-x＞0，因为当，时，f（x）=sin2x+cosx，
所以f（-x）=sin（-2x）+cos（-x）=-sin2x+cosx，
因为f（x）为定义在R上的奇函数，
所以f（x）=-f（-x）=sin2x-cosx，
综上得，f(x)=
|
故答案为：f(x)=
|
点评：本题考查利用函数的奇偶性求函数的解析式，易忘f（0）=0，属于基础题．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
已知（1+bi）2=2i（b∈R，i是虚数单位），则b=（ ）
| A、2 | B、1 | C、±1 | D、1或2 |
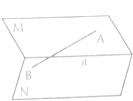二面角M-a-N中，点A∈M，点B∈N，AB=4