题目内容
“a>2”是“关于x的不等式|x+1|+|x-1|≤a的解集非空”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据绝对值不等式的性质,利用充分条件和必要条件的定义进行判断即可得到结论.
解答:
解:若关于x的不等式|x+1|+|x-1|≥2,
则要使关于x的不等式|x+1|+|x-1|≤a的解集非空,则a≥2,
∴当“a>2”是“关于x的不等式|x+1|+|x-1|≤a的解集非空”的充分不必要条件,
故选:A
则要使关于x的不等式|x+1|+|x-1|≤a的解集非空,则a≥2,
∴当“a>2”是“关于x的不等式|x+1|+|x-1|≤a的解集非空”的充分不必要条件,
故选:A
点评:本题主要考查充分条件和必要条件的判断,根据绝对值的性质是解决本题的关键,比较基础.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
函数y=sinx-cosx的图象可由函数y=sinx+cosx的图象经过下列哪种变换得到( )
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
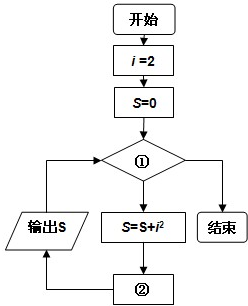 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
设变量x,y满足不等式组
,则2x+3y的最大值等于( )
|
| A、1 | B、10 | C、41 | D、50 |
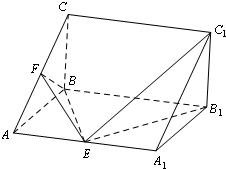 如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=
如图,在三菱柱ABC-A1B1C1中,AA1B1B为矩形,平面AA1B1B⊥平面ABC.∠ABC=90°,AB=BC=