题目内容
6.弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是$\frac{2}{sin1}$.分析 解直角三角形AOC,求出半径AO,代入弧长公式求出弧长的值.
解答  解:如图:∠AOB=2,过点0作OC⊥AB,C为垂足,并延长OC交 $\widehat{AB}$于D,
解:如图:∠AOB=2,过点0作OC⊥AB,C为垂足,并延长OC交 $\widehat{AB}$于D,
∠AOD=∠BOD=1,AC=$\frac{1}{2}$AB=1,
Rt△AOC中,AO=$\frac{AC}{sin∠AOC}$=$\frac{1}{sin1}$,
从而弧长为α•r=$\frac{2}{sin1}$.
故答案为:$\frac{2}{sin1}$.
点评 本题考查弧长公式的应用,解直角三角形求出扇形的半径AO的值,是解决问题的关键,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
5.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
(Ⅰ)在答题纸上列出这些数据的频率分布表,并作出频率分布直方图;
(Ⅱ)估计这种产品质量指标值的平均值及中位数(中位数的数值保留到小数点后一位).
| 质量指标 值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(Ⅱ)估计这种产品质量指标值的平均值及中位数(中位数的数值保留到小数点后一位).
17.已知集合M={x|x(4-x)<0},N={x|(x-1)(x-6)<0,x∈Z},则M∩N=( )
| A. | (1,6) | B. | (4,6) | C. | {4,5,6} | D. | {5} |
1.椭圆$\frac{x^2}{9}+\frac{y^2}{2}=1$的焦点为F1,F2,点P在椭圆上,若|PF1|=2,则∠F1PF2=( )
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
15.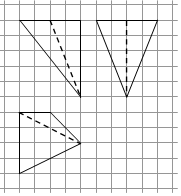 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为( )| A. | 15 | B. | 16 | C. | $\frac{50}{3}$ | D. | $\frac{53}{3}$ |