题目内容
（1）若
=（1，0），
=（-1，1），
=
+（
•
）
，求|
|；
（2）已知|
|=1，|
|=
，|
+
|=1，求
与
夹角θ的值．
| a |
| b |
| c |
| a |
| a |
| b |
| b |
| c |
（2）已知|
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算,平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）利用向量的数量积运算性质和模的计算公式即可得出；
（2）利用向量数量积的性质及其特殊角的三角函数值即可得出．
（2）利用向量数量积的性质及其特殊角的三角函数值即可得出．
解答：
解：（1）∵
=(1，0)，
=（-1，1），
•
=-1，
∴
=
+(
•
)
=（1，0）-（-1，1）=（2，-1），
∴|
|=
=
．
（2）∵|
+
|=
=
=1，
∴cosθ=-
，
∵θ∈[0，π]，∴θ=
．
| a |
| b |
| a |
| b |
∴
| c |
| a |
| a |
| b |
| b |
∴|
| c |
| 22+(-1)2 |
| 5 |
（2）∵|
| a |
| b |
|
12+(
|
∴cosθ=-
| ||
| 2 |
∵θ∈[0，π]，∴θ=
| 5π |
| 6 |
点评：本题考查了向量的数量积运算性质和模的计算公式，属于基础题．
练习册系列答案
相关题目
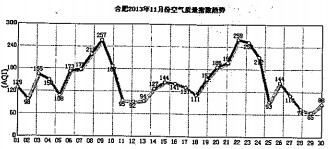合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图．