题目内容
有4名同学参加唱歌、跳舞、下棋三项比赛,每项比赛至少有一人参加,每人只能参加一项比赛,另外甲同学不能参加跳舞比赛,则不同的参赛方案的种数为 (用数字作答)
考点:计数原理的应用
专题:应用题,排列组合
分析:分类讨论,跳舞1人,2人,根据分类计数原理得到结果.
解答:
解:因为将4名学生参加三项比赛,那么每项比赛至少有1人参加,则将4=1+1+2,同时由于甲同学不能参加跳舞比赛,因此可以分为两类,参加跳舞的只有一个人时,那么先选出一个人,有3种方法,然后将其与三个人分组为3=1+2,所有的情况有
,利用分步乘法计数原理得到为3
=18种,
同时参加跳舞的有两个人时,则有3种方法,剩余的参加的比赛分组分配有
,利用乘法计数原理可知共有3
=6,结合分类计数加法原理得到为18+6=24,
故答案为:24.
| C | 1 3 |
| C | 2 2 |
| A | 2 2 |
| C | 1 3 |
| C | 2 2 |
| A | 2 2 |
同时参加跳舞的有两个人时,则有3种方法,剩余的参加的比赛分组分配有
| A | 2 2 |
| A | 2 2 |
故答案为:24.
点评:本题考查分类计数问题,解题的关键是正确分类,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
若a>0,b>0,则有( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某班级有6名同学去报名参加校学生会的4项社团活动,若甲、乙两位同学不参加同一社团,每个社团都有人参加,每人只参加一个社团,则不同的报名方案数为( )
| A、4320 | B、2400 |
| C、2160 | D、1320 |
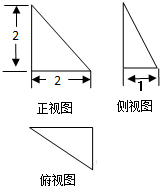 已知某几何体的三视图如图所示,三个视图都为直角三角形,其中主视图是以2为直角边的等腰直角三角形,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,三个视图都为直角三角形,其中主视图是以2为直角边的等腰直角三角形,则该几何体的外接球的表面积为( )| A、16π | B、9π | C、8π | D、4π |