题目内容
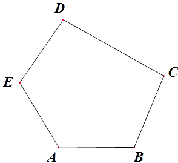如图所示，一个确定的凸五边形 ABCDE，令x=| AB |
| AC |
| AB |
| AD |
| AB |
| AE |
考点：平面向量数量积的运算,向量在几何中的应用
专题：平面向量及应用
分析：根据向量的数量积公式分别判断x，y，z的符号，得到大小关系．
解答：
解：由题意，x=
•
=AB×ACcos∠BAC＞0，
y=
•
=AB×ADcos∠BAD≈AB×ACcos∠BAD，
又∠BAD＞∠BAC
所以cos∠BAD＜cos∠BAC，
所以x＞y＞0
z=
•
=AB×AEcos∠BAE＜0，
所以x＞y＞z．
故答案为：x＞y＞z．
| AB |
| AC |
y=
| AB |
| AD |
又∠BAD＞∠BAC
所以cos∠BAD＜cos∠BAC，
所以x＞y＞0
z=
| AB |
| AE |
所以x＞y＞z．
故答案为：x＞y＞z．
点评：本题考查了向量的数量积的公式；属于基础题．
练习册系列答案
相关题目
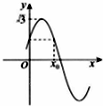已知f（x）=Asin（2x+