题目内容
复数z=
，则图中表示z的共轭复数的点是（ ）
| 2 |
| i-1 |
| A、A | B、B | C、C | D、D |
考点：复数的基本概念
专题：数系的扩充和复数
分析：利用复数的运算法则和共轭复数的定义、复数的几何意义即可得出．
解答：
解：z=
=
=
=-1-i，
∴
=-1+i表示的点是（-1，1）．
因此图中表示z的共轭复数的点是A．
故选：A．
| 2 |
| i-1 |
| -2(i+1) |
| (i-1)(-1-i) |
| -2(1+i) |
| 2 |
∴
. |
| z |
因此图中表示z的共轭复数的点是A．
故选：A．
点评：本题考查了复数的运算法则和共轭复数的定义、复数的几何意义，属于基础题．
练习册系列答案
相关题目
对于每个非零自然数n，抛物线y=x2-
x+
与x轴交于An、Bn两点，以AnBn表示这两点间的距离，则A1B1+A2B2+…+A2014B2014的值是（ ）
| 2n+1 |
| n2+n |
| 1 |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
D、
|
点P（x，y）为不等式组
表示的平面区域上一点，则x+2y取值范围为（ ）
|
A、[-
| ||||
B、[-2，
| ||||
| C、[-1，2] | ||||
| D、[-2，2] |
已知a，b∈R且a≠b，若aea=beb（e为自然对数的底数），则下列正确的是（ ）
| A、lna-lnb=b-a |
| B、lna-lnb=a-b |
| C、ln（-a）-ln（-b）=b-a |
| D、ln（-a）-ln（-b）=a-b |
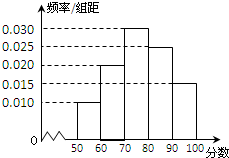某中学从某次考试成绩中抽取若干名学生的分数，并绘制成如图的频率分布直方图．样本数据分组为[50，60），[60，70），[70，80），[80，90），[90，100]．若用分层抽样的方法从样本中抽取分数在[80，100]范围内的数据16个，则其中分数在[90，100]范围内的样本数据有（ ）