题目内容
设函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+2x+b(b为常数),则f(-1)= .
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:由奇函数的性质得f(0)=0,代入解析式求出b的值,利用函数的奇偶性将f(-1)转化为f(-1)=-f(1),然后直接代入解析式即可.
解答:
解:∵函数f(x)为定义在R上的奇函数,
∴f(0)=1+b=0,解得b=-1,
则当x≥0时,f(x)=3x+2x-1,
∴f(-1)=-f(1)=-(3+2-1)=-4,
故答案为:-4.
∴f(0)=1+b=0,解得b=-1,
则当x≥0时,f(x)=3x+2x-1,
∴f(-1)=-f(1)=-(3+2-1)=-4,
故答案为:-4.
点评:本题考查了奇函数的结论:f(0)=0的灵活应用,以及函数奇偶性的应用,利用函数的奇偶性将f(-1)转化到已知条件上求解.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
复数z=
,则图中表示z的共轭复数的点是( )

| 2 |
| i-1 |

| A、A | B、B | C、C | D、D |
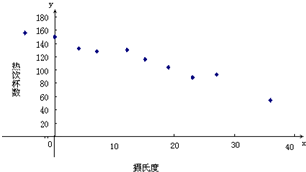 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程 |
| y |
| A、气温与热饮的销售杯数之间成正相关 | ||
| B、当天气温为2°C时,这天大约可以卖出143杯热饮 | ||
| C、当天气温为10°C时,这天恰卖出124杯热饮 | ||
D、由于x=0时,
|
一个几何体的三视图如图所示,则该几何体的体积是( )


| A、8 | B、10 | C、12 | D、14 |