题目内容
18.从双曲线C:b2x2-a2y2=a2b2(a>0,b>0)的左焦点F1引圆x2+y2=a2的切线为T,且l交双曲线的右支于点P,若点T是线段F1P的中点,则双曲线C的渐近线方程为2x±y=0.分析 由已知可得:丨OT丨=a,设双曲线的右焦点为F′,由T为线段FP的中点,知|PF′|=2a,|PF|=2b,由双曲线的定义知:2b-2a=2a,由此能求出双曲$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的渐近线方程.
解答 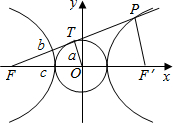 解:∵过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,
解:∵过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左焦点F引圆x2+y2=a2的切线,切点为T,
∴丨OT丨=a,
设双曲线的右焦点为F′,
∵T为线段FP的中点,
∴|PF′|=2a,|PF|=2b,
由双曲线的定义知:2b-2a=2a,
∴b=2a.
∴双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的渐近线方程为bx±ay=0,
即2ax±ay=0,
∴2x±y=0.
故答案为:2x±y=0.
点评 本题考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
8.$g(x)=x+\frac{1}{x}$上各点处的切线倾斜角为α,则α的取值范围( )
| A. | (0,π) | B. | $({0,\frac{π}{4}})$ | C. | $[{0,\frac{π}{4}})∪({\frac{3}{4}π,π})$ | D. | $[{0,\frac{π}{4}})∪({\frac{π}{2},π})$ |
7.$\overrightarrow{AB}$+$\overrightarrow{AC}$-$\overrightarrow{BC}$+$\overrightarrow{BA}$ 化简后等于( )
| A. | 3$\overrightarrow{AB}$ | B. | $\overrightarrow{BA}$ | C. | $\overrightarrow{AB}$ | D. | $\overrightarrow{CA}$ |
8.已知两个等差数列{an}和{bn}的前n项和之比为$\frac{7n+1}{4n+27}(n∈{N^*})$,则$\frac{{{a_{11}}}}{{{b_{11}}}}$等于( )
| A. | $\frac{78}{71}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{7}{4}$ |