题目内容
13.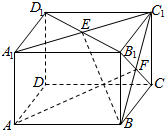 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出E、F两点间的距离.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
∵在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,
E、F分别是面A1B1C1D1、面BCC1B1的中心,
由题意得E(1,1,$\sqrt{2}$),F(1,2,$\frac{\sqrt{2}}{2}$),
∴E、F两点间的距离:
|EF|=$\sqrt{(1-1)^{2}+(2-1)^{2}+(\frac{\sqrt{2}}{2}-\sqrt{2})^{2}}$=$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查空间中两点间距离的求法,是基础题,解题时要认真审题,注意空间中两点间距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.对任意实数x,y,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,那么对定义域R上的函数f(x),下列结论正确的是( )
| A. | f(x)是奇函数,又是减函数 | B. | f(x)是奇函数,又是增函数 | ||
| C. | f(x)是偶函数,又是减函数 | D. | f(x)是偶函数,又是增函数 |
17.已知函数f(x)=$\left\{\begin{array}{l}{{ax}^{2}+2x+1,(-2<x≤0)}\\{ax-3,(x>0)}\end{array}\right.$有3个零点,则实数a的取值范围是( )
| A. | ($\frac{3}{4}$,1) | B. | ($\frac{1}{4}$,1) | C. | (0,1) | D. | (-∞,1) |