题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{ax}^{2}+2x+1,(-2<x≤0)}\\{ax-3,(x>0)}\end{array}\right.$有3个零点,则实数a的取值范围是( )| A. | ($\frac{3}{4}$,1) | B. | ($\frac{1}{4}$,1) | C. | (0,1) | D. | (-∞,1) |
分析 令f(x)在(-2,0]上有2个零点,在(0,+∞)上有1个零点,根据函数类型及零点范围及个数列出不等式组,解出a的范围.
解答 解:∵f(x)由3个零点,∴f(x)在(-2,0]上有2个零点,在(0,+∞)上有1个零点.
∴$\left\{\begin{array}{l}{4a-4+1>0}\\{-2<-\frac{1}{a}<0}\\{\frac{4a-4}{4a}<0}\\{a>0}\end{array}\right.$,解得$\frac{3}{4}$<a<1.
故选:A.
点评 本题考查了函数零点的个数判断,分段函数的应用,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
2.已知集合A={x|x2-2x-3≤0},B={y|y=x2,x∈R},则A∩B=( )
| A. | ∅ | B. | [0,1] | C. | [0,3] | D. | [-1,+∞) |
9.已知集合A={1,2},B={1,m,3},如果A∩B=A,那么实数m等于( )
| A. | -1 | B. | 0 | C. | 2 | D. | 4 |
6.抛物线y=2x2的焦点坐标是( )
| A. | (0,$\frac{1}{8}$) | B. | ($\frac{1}{4}$,0) | C. | (1,0) | D. | (0,$\frac{1}{4}$) |
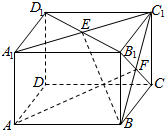 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.