题目内容
2.函数f(x)=$\sqrt{{x}^{2}-2x+5}$+$\sqrt{{x}^{2}+6x+10}$的最小值.分析 由配方可得函数表示f(x)表示P(x,0)到两点A(1,2),B(-3,1)的距离之和.作出点A关于x轴的对称点A'(1,-2),连接A'B,交x轴于P,运用两点之间线段最短,由两点的距离公式计算即可得到.
解答 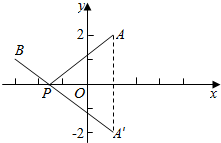 解函数f(x)=$\sqrt{{x}^{2}-2x+5}$+$\sqrt{{x}^{2}+6x+10}$
解函数f(x)=$\sqrt{{x}^{2}-2x+5}$+$\sqrt{{x}^{2}+6x+10}$
=$\sqrt{(x-1)^{2}+{2}^{2}}$+$\sqrt{(x+3)^{2}+{1}^{2}}$,
设点P(x,0),A(1,2),B(-3,1),
则f(x)表示P到两点A,B的距离之和.
作出点A关于x轴的对称点A'(1,-2),
连接A'B,交x轴于P,
则||PA|+|PB|=|PA'|+|PB|≥|A'B|=$\sqrt{(1+3)^{2}+(-2-1)^{2}}$=5,
则当A,P,B'三点共线,取得最小值5,
则函数f(x)的最小值为5.
点评 本题考查函数的最值的求法,注意运用几何方法:对称法,两点间的距离公式,属于中档题.

练习册系列答案
相关题目
12.设Sn为等比数列{an}的前n项和,且8a3+a6=0,则$\frac{S_4}{S_2}$=( )
| A. | -11 | B. | -8 | C. | 5 | D. | 11 |
10.已知函数f(x)=x3-bx2-4,x∈R,则下列命题正确的是( )
| A. | 当b>0时,?x0<0,使得f(x0)=0 | |
| B. | 当b<0时,?x<0,都有f(x)<0 | |
| C. | f(x)有三个零点的充要条件是b<-3 | |
| D. | f(x)在区间(0.+∞)上有最小值的充要条件是b<0 |
6.抛物线y=2x2的焦点坐标是( )
| A. | (0,$\frac{1}{8}$) | B. | ($\frac{1}{4}$,0) | C. | (1,0) | D. | (0,$\frac{1}{4}$) |
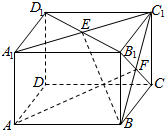 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.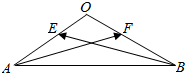 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.