题目内容
5.函数y=1g(3+2x-x2)的定义域为集合M.求:当x∈M时,函数f(x)=2x+3-3•4x的最值,并指出f(x)取得最值时的x值.分析 由对数函数的定义域,可得M,可设t=2x($\frac{1}{2}$<t<8),可得y=8t-3t2,再由二次函数的值域求法,可得最值.
解答 解:由y=1g(3+2x-x2),
可得3+2x-x2>0,解得-1<x<3,
即M=(-1,3),
函数f(x)=2x+3-3•4x的,
可设t=2x($\frac{1}{2}$<t<8),
可得y=8t-3t2=-3(t-$\frac{4}{3}$)2+$\frac{16}{3}$,
当t=$\frac{4}{3}$,即x=log2$\frac{4}{3}$时,函数取得最大值$\frac{16}{3}$,
无最小值.
点评 本题考查函数的最值的求法,注意运用换元法和对数函数、指数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=x3-bx2-4,x∈R,则下列命题正确的是( )
| A. | 当b>0时,?x0<0,使得f(x0)=0 | |
| B. | 当b<0时,?x<0,都有f(x)<0 | |
| C. | f(x)有三个零点的充要条件是b<-3 | |
| D. | f(x)在区间(0.+∞)上有最小值的充要条件是b<0 |
9.已知集合A={1,2},B={1,m,3},如果A∩B=A,那么实数m等于( )
| A. | -1 | B. | 0 | C. | 2 | D. | 4 |
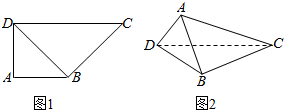 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.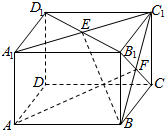 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=$\sqrt{2}$,E、F分别是面A1B1C1D1、面BCC1B1的中心,则E、F两点间的距离为$\frac{\sqrt{6}}{2}$.