题目内容
已知圆M：（x-3）2+y2=9，过圆心M的直线与抛物线y2=12x和圆M的交点自上而下依次为点A，B，C，D，则
•
的值是 ．
| AB |
| CD |
考点：平面向量数量积的运算,圆的标准方程
专题：平面向量及应用
分析：设出点A、B、C、D的坐标，然后，联立方程组，写出向量的响应坐标形式，然后，求解即可．
解答：
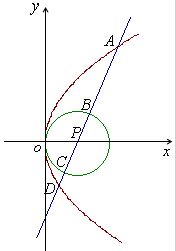解：如图所示：
圆M的方程为：（x-3）2+y2=9，则其直径长|BC|=6，圆心为P（3，0），
设l的方程为ky=x-3，即x=ky+3，代入抛物线方程得：y2=12ky+36，
∴y2-12ky-36=0，
设A（x1，y1），D（x2，y2），
∴y1+y2=12k，y1y2=-36，
设B（x3，y3），C（x4，y4），
将直线方程x=ky+3代人圆的方程（x-3）2+y2=9，得
y=±
，x=±
+3，
∵
=(x3-3，y3)，
=(x2-3，y2)，
=(x4-3，y4)，
=(x1-3，y1)，
∴
•
=（
-
）•（
-
）
=
•
-
•
-
•
+
•
=（x1-3）（x3-3）+y1y3-（x3-3）（x4-3）+y3y4-（x1-3）（x2-3）-y1y2+（x1-3）（x4-3）+y1y4=9．
故答案为：9．
解：如图所示：圆M的方程为：（x-3）2+y2=9，则其直径长|BC|=6，圆心为P（3，0），
设l的方程为ky=x-3，即x=ky+3，代入抛物线方程得：y2=12ky+36，
∴y2-12ky-36=0，
设A（x1，y1），D（x2，y2），
∴y1+y2=12k，y1y2=-36，
设B（x3，y3），C（x4，y4），
将直线方程x=ky+3代人圆的方程（x-3）2+y2=9，得
y=±
| 3 | ||
|
| 3k | ||
|
∵
| PB |
| PD |
| PC |
| PA |
∴
| AB |
| CD |
| PB |
| PA |
| PD |
| PC |
=
| PB |
| PD |
| PB |
| PC |
| PA |
| PD |
| PA |
| PC |
=（x1-3）（x3-3）+y1y3-（x3-3）（x4-3）+y3y4-（x1-3）（x2-3）-y1y2+（x1-3）（x4-3）+y1y4=9．
故答案为：9．
点评：本题考查直线与圆、抛物线的位置关系，考查学生的计算能力，应用向量的坐标表示是关键，属于中档题．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
已知四棱锥P-ABCD，底面ABCD是菱形，且PC⊥底面ABCD，E是侧棱PC上的动点．设P是椭圆
+
=1上的点，若F1，F2是椭圆的两个焦点，过F1的直线交椭圆于A、B两点，则△F2AB的周长等于（ ）
| x2 |
| 16 |
| y2 |
| 9 |
| A、8 | B、12 | C、16 | D、32 |
若m是5和
的等比中项，则圆锥曲线
+y2=1的离心率是（ ）
| 16 |
| 5 |
| x2 |
| m |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如图，设四棱锥E-ABCD的底面为菱形，且∠ABC=60°，AB=EC=2，AE=BE=